Os gases que se desviarem do comportamento ideal são conhecidos como gases reais, não cumprem a equação dos gases reais. Eles se originam em dois fatores:
- A teoria diz que, à medida que a pressão aumenta o volume de gás se torna menor e se aproxima de zero. Embora se aproxime de um pequeno número, não será zero porque as moléculas ocupam espaço (ou seja, têm volume) e não podem ser comprimidas.
- Há forças intermoleculares nos gases. Essas forças se tornam cada vez mais importantes a baixas temperaturas, onde o movimento de tradução das moléculas diminui, quase para parar. No entanto, em altas temperaturas, ou mesmo em temperaturas normais, as forças intermoleculares são muito pequenas e tendem a ser consideradas insignificantes.
Introdução
Enquanto a teoria cinética- molecular faz Um excelente trabalho explicando os gases, existem algumas propriedades que não explicam sobre sua descrição dos gases reais. A teoria assume que as colisões entre moléculas de gás e as paredes de um recipiente são perfeitamente elásticas, as partículas de gás não têm volume e sem repulsão ou forças de atração entre moléculas. Essas suposições se referem aos gases ideais. Embora estas suposições sejam geralmente verdadeiras, há circunstâncias em que os gases se desviam do comportamento ideal.
Gás tendem a se comportar idealmente em duas situações diferentes:
- Idealmente envolva alta Temperaturas: Isto é devido ao fato de que moléculas voam umas com as outras em velocidades extremamente altas (devemos lembrar que a temperatura é uma medida de energia cinética média, que é diretamente proporcional à velocidade).
- se comportar idealmente em Pressões baixas: Isso é porque a baixas pressões, o volume de moléculas tende a ser insignificante em comparação com o volume total de gás (lembre-se que a lei de Boyle diz que a pressão e o volume são inversamente proporcionais).
Quando você se comporta de maneira não-ideal?
O gás é comportado de maneira não ideal (ou real) a temperaturas frias devido ao fato de que em temperaturas frias, moléculas se movem l Inicialmente, permitindo que as forças de repulsão ou atração entrem em vigor, desviando do comportamento de um gás ideal. Os gases também se comportam de grandes pressões, porque em altas pressões, o volume de moléculas se torna um fator.
Gases reais e volume molar
para ilustrar as pequenas diferenças entre o Propriedades numéricas de gases reais e ideais em temperaturas e pressões normais, considere a seguinte comparação. Você se lembrará de que usamos a equação de gás ideal para calcular um valor para o volume molar de um gás ideal em condições normais de pressão e temperatura.
Se a densidade de um gás é conhecida em uma determinada temperatura e pressão , Calcule seu volume molar será relativamente fácil. Por exemplo: com uma pressão 1 ATM para 273 K, a densidade de hélio é de 0,1785 g / l. Isso significa que 0,1785 g de hélio ocupa 1 litro sob pressão normal e condições de temperatura (1 atmosfera e 273 K). Em seguida, para calcular o volume molar, por exemplo, o hélio:
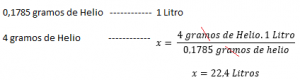
| Volume molar (litros) | ele | 0.1785 | 22.4 | |
| n2 | 1.2506 | 22.4 | ||
| O2 | ||||
| CH4 | 0.717 | 22.3 | ||
| CO2 | ||||
| c2H4 | 1.260 | 22.2 | ||
| NH3 | 0.769 | 22.1 | ||
| SO2 | 2.926 | 21.9 |
Embora para cálculos simples, usamos o valor 22.4 litros para todos os gases pode ser visto que não é exatamente verdade. Mesmo em temperaturas normais e pressões, os gases reais podem se desviar ligeiramente do comportamento ideal. O desvio é muito maior em condições mais extremas, como veremos abaixo:
fatores de compressão
para um gás ideal, PV = NRT. É cumprido que, ao dividir o PV / NRT = 1.
Para gases reais, isso só é possível em baixas pressões (menos de 5 atmosferas). Analisando o gráfico é observado que o desvio se torna mais pronunciado com o aumento da pressão. E aumentando a temperatura o gás leva um comportamento próximo ao ideal.
Em um gás real, à medida que a pressão aumenta, o quociente entre PV / NRR aumenta para um número maior que um, (PV / NRT > 1) distorcendo a idealidade. O mesmo acontece quando uma temperatura diminui, já que o fator compressivo aumenta acima de 1 (PV / NRT > 1) à medida que a temperatura se aproxima de um número menor.
um ideal O gás tem um fator de compressibilidade igual a um, mas o fator de compressibilidade para um gás real pode variar muito a partir desse número. Os gráficos abaixo mostram como isso varia para o nitrogênio como você altera a temperatura e pressão.
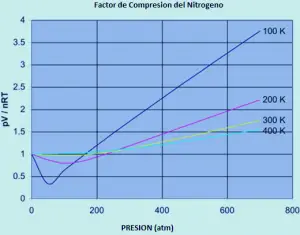
Se o nitrogênio era um gás ideal em todas as condições de temperatura e pressão, cada uma dessas curvas seria uma linha reta horizontal que mostraria um fator de compressão de 1. (claro que isso é obviamente verdadeiro).
Para ser levado em conta
em baixas pressões de aproximadamente um pouco menos de 1 atmosfera, o fator de compressão aproxima-se 1. O nitrogênio aborda o comportamento ideal para pressões comuns. O comportamento não ideal piora temperaturas. Para temperaturas de 300 ou 400 k, o fator de compressão se aproxima de 1 em uma ampla gama de pressões. O nitrogênio torna-se mais ideal em uma faixa de pressão maior à medida que a temperatura aumenta.
O comportamento não ideal piora pressões mais altas. Deve haver pelo menos um efeito que torna a proporção PV / NRR. Muito baixa, especialmente a baixas temperaturas. E deve haver pelo menos um efeito que tenha que aumentar muito à medida que a pressão aumenta.
é o mesmo comportamento manifestado com outros gases?
O gráfico a seguir mostra como os fatores de compressão variam com a pressão para uma variedade de gases a uma temperatura fixa de 273k.
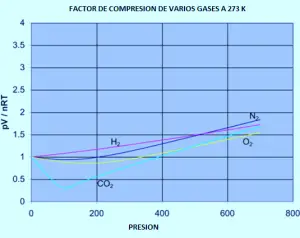
Se tiver que refazer o conjunto dos gráficos originais de nitrogênio (a temperaturas variáveis) para qualquer um desses outros gases, você descobriria que cada um deles produzirá um conjunto de curvas semelhantes às do nitrogênio. O que varia é a temperatura na qual as diferentes formas gráficas são produzidas. Por exemplo, se o gráfico de dióxido de carbono for observado em 273 K (gráfico anterior), é semelhante ao nitrogênio a 100 K do primeiro conjunto de curvas, embora não aumente tão pronunciado em pressões mais altas.
É fácil dizer que os gases se tornam menos ideais a baixas temperaturas, mas o que tem uma temperatura baixa varia de um gás para outro. Quanto mais próximo da temperatura na qual o gás é convertido em líquido (ou, no caso de dióxido de carbono, em um sólido), quanto mais não é ideal o gás se torna.
O que causa o comportamento não ideal ?
Nas suposições que fazemos sobre os gases ideais, existem duas afirmações que dizem coisas que não podem ser verdadeiras de um gás real, e elas têm um efeito sobre a pressão e o volume.
O problema do volume:
A teoria cinética supõe que, para um gás ideal, o volume ocupado pelas próprias moléculas é totalmente insignificante em comparação com o volume do recipiente. Para um gás real (real), essa suposição não é verdadeira. As próprias moléculas ocupam uma parte do espaço no recipiente. O espaço no recipiente está disponível para que as coisas se movam seja menor que o volume medido do contêiner.
Na imagem, a teoria cinética assume que todo esse espaço está disponível para que as moléculas se movam para dentro. Mas, na verdade, como visto na imagem (b), apenas essa quantidade de espaço está disponível, porque o restante do volume é ocupado pelas próprias moléculas.
Se a pressão estiver baixa, o volume ocupado pelas moléculas reais é insignificante em comparação com o volume total do contêiner.Mas, à medida que o gás comprime, a proporção do volume total que as próprias moléculas ocupam aumentadas cada vez mais. Imagine que você está comprimindo tanto o gás que as moléculas se tocam. Nesse ponto, o volume disponível para que as moléculas se movam seja zero.
Suponha que, a uma alta pressão, o volume do contêiner é 1000 cm3, mas assumindo que as moléculas ocupam até 100 cm3 dela. / p>
A equação de gás ideal foi desenvolvida fazendo cálculos com base na hipótese dos teóricos cinéticos. Supõe-se que v em PV é o volume disponível para que as moléculas possam se mover livremente, mas neste caso seriam apenas 900 cm3, não 1000 cm3.
Se nós calculamos o fator de compressão, PV / NRT, colocando o Recipiente total de volume na fórmula, o valor que obteremos como resultado será maior do que deveria ser (já que o volume real deve ser de 900 cm3).
Para um gás real, como nitrogênio, observe como O fator de compressão tende a aumentar com a pressão, enquanto para um gás ideal, o fator de compressão seria de 1 a qualquer valor de pressão.

O valor do fator de compressão é muito alto em altas pressões para um gás real. A razão para isso é que o volume medido que usamos na expressão PV / NRT é muito alto (nos lembramos do caso anterior) e não levamos em conta o volume ocupado pelas moléculas. Esse erro mostra mais quando o gás é compactado.
O problema de pressão:
Outra hipótese da teoria cinética para os gases ideais é que não há forças intermoleculares entre as moléculas. Isso é errado, já que nos gases reais não é assim. Se não houvesse forças intermoleculares, seria impossível condensar o gás como um líquido. Mesmo o hélio, que tem a menor de todas as forças intermoleculares, pode se tornar um líquido se a temperatura for baixa o suficiente.
Que efeito as forças intermoleculares têm? Para uma molécula de gás que está no centro do recipiente, não haverá efeito não (imagem a). As moléculas atrairão até certo ponto onde essas atrações são canceladas umas às outras. As atrações exercidas pela molécula de volta tendem a desacelerar e serão canceladas pelas atrações das moléculas na frente dela, tendendo a acelerar (ambas as atrações).
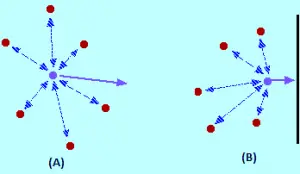
A molécula continuará se movendo na mesma direção na mesma velocidade, mas quando estiver atingindo o contêiner, o seguinte ocorre: como não há Moléculas na frente dele, o cancelamento de atrações intermoleculares não é produzido. Portanto, a molécula começa a diminuir sua velocidade antes de bater com a parede do recipiente (imagem B). Consequentemente, colidirá com a parede com menos força e menor pressão.
O efeito geral disso é o culpado que a pressão é menor do que seria se o gás era ideal. Isso significa que, se a pressão medida na expressão PV / NRR for colocada, o valor do fator de compressão será menor do que se o gás for ideal. Esta é a razão pela qual, sob algumas condições, os gráficos dos fatores de compressão estão abaixo do valor ideal de 1. Vamos ver novamente o exemplo de nitrogênio (se eu já souber, você está cansado do gráfico haha).

Este efeito é mais importante em baixas temperaturas. Porque? Em baixas temperaturas, as moléculas se movem mais lentamente. Em temperaturas mais altas, onde as moléculas se movem muito mais rápido, qualquer pequeno para trás da molécula para o centro do gás mal avisará. Em altas temperaturas, o efeito das forças intermoleculares é certamente insignificante, uma vez que as moléculas escapam das interações.
E há um efeito final sobre as forças intermoleculares, que é ligeiramente oculto. Como a pressão aumenta, as moléculas são mais juntas. Se eles estão mais próximos, as forças intermoleculares serão mais importantes.
Qual é o gás mais ideal?
devemos procurar um gás cujas moléculas são as menores, e onde as forças intermoleculares são muito baixas. Esse gás seria hélio. Uma molécula de hélio tem um único átomo que é muito pequeno, e as forças de dispersão van der waals são muito baixas.
como hélio, uma molécula de hidrogênio também tem dois elétrons, para que as forças intermoleculares sejam pequeno (mas não tão pequeno quanto o hélio). Na molécula de hidrogênio, você tem dois átomos nos quais você pode distribuir as cargas.À medida que as moléculas se tornam maiores, as forças de dispersão aumentarão, e você pode obter outras forças intermoleculares, como atrações dipolo-dipolo. Os gases feitos de moléculas como estes serão muito menos ideais.
A equação van der Waals
Há um grande número de equações que podem descrever como os gases reais agem, mas para fazer É simples, os químicos aderem à equação van der waals porque é o mais fácil descrever como os gases agem:
p é a pressão em atmosferas (ATM)
V é o volume em litros (l)
n é o número de moles (mol)
A é apenas uma constante de proporcionalidade
B Também é uma constante de proporcionalidade
Tenha em mente que é muito semelhante à equação de gás ideal, mas corrige algumas coisas.
O lado direito da equação é exatamente o mesmo que a equação de gás ideal. Só muda em relação à pressão e volume para perceber as coisas em relação às forças intermoleculares e o volume de moléculas de gás.
no lado esquerdo explica uma pressão mais baixa do que a de um gás ideal, uma vez que leva em conta correções que ocorrem quando as moléculas suavizam o impacto das outras moléculas das interações intermoleculares.