Els gasos que es desvien de l’comportament ideal són coneguts com a gasos reals, no compleixen amb l’equació d’estat dels gasos reals .. S’originen en dos factors:
- la teoria diu que a mesura que augmenta la pressió el volum de gas es torna mes petit i s’apropa a zero. Encara s’acosta a un nombre petit, no serà zero perquè les molècules ocupen espai (és a dir, tenen volum) i no poden ser comprimides.
- Hi ha forces intermoleculars en els gasos. Aquestes forces es tornen cada vegada més importants en temperatures baixes, on el moviment traslacional de les molècules disminueix, gairebé fins aturar-se. No obstant això, a altes temperatures, o fins i tot a temperatures normals, les forces intermoleculars són molt petites i tendeixen a considerar-se insignificants.
Introducció
Mentre que la Teoria Cinética- molecular fa un excel·lent treball explicant els gasos, hi ha algunes propietats que no explica pel que fa a la seva descripció dels gasos reals. La teoria assumeix que les col·lisions entre molècules de gas i les parets d’un contenidor són perfectament elàstiques, les partícules de gas no tenen cap volum i no hi ha forces de repulsió o d’atracció entre molècules. Aquestes suposicions es refereixen als gasos ideals. Si bé aquestes suposicions generalment són certes, hi ha circumstàncies en què els gasos es desvien de l’comportament ideal.
Els gasos tendeixen a comportar-idealment en dues situacions diferents:
- Es comporten idealment a altes temperatures: Això es deu a el fet que les molècules volen unes sobre altres a velocitats extremadament altes (hem de recordar que la temperatura és una mesura de l’energia cinètica mitjana, que és directament proporcional a la velocitat).
- es comporten idealment a pressions baixes: Això es deu al fet que a baixes pressions, el volum de les molècules tendeix a ser insignificant en comparació amb el volum total de gas (recordar que la Llei de Boyle diu que la pressió i el volum són inversament proporcionals).
¿quan es comporten de manera no ideal?
Els gasos es comporten de manera no ideal (o real) a temperatures fredes a causa de l’ fet que a temperatures fredes, les molècules es mouen l entamente, permetent que les forces de repulsió o d’atracció tinguin efecte, desviant-se de l’comportament d’un gas ideal. Els gasos també es comporten de forma no ideal a altes pressions, perquè a altes pressions, el volum de molècules esdevé un factor.
Gasos reals i volum molar
Per il·lustrar les petites diferències entre les propietats numèriques dels gasos reals i ideals a temperatures i pressions normals, consideri la següent comparació. Recordarà que fem servir l’equació de gas ideal per calcular un valor per al volum molar d’un gas ideal en condicions normals de pressió i temperatura.
Si es coneix la densitat d’un gas a una temperatura i pressió determinada, calcular el seu volum molar serà relativament fàcil. Per exemple: Amb una pressió 1 atm a 273 K, la densitat de l’heli és de 0,1785 g / l. Això vol dir que 0,1785 g d’heli ocupa 1 Litre en condicions normals de pressió i temperatura (1 atmosfera i 273 K). Llavors per calcular el volum molar, per exemple de l’Heli: amor 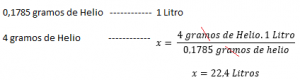
| Densitats dels gasos i Volum Molar (a condicions normals de pressió i temperatura) | ||
| Densitat (g / L) | Volum Molar (Litres) | |
| He | 0,1785 | 22.4 |
| N2 | 1.2506 | 22.4 |
| O2 | 1.4290 | 22.4 |
| CH4 | 0.717 | 22.3 |
| CO2 | 1.977 | 22.3 |
| C2H4 | 1.260 | 22.2 |
| NH3 | 0769 | 22.1 |
| SO2 | 2.926 | 21.9 |
Encara que per als càlculs senzills fem servir el valor 22,4 Litres per a tots els gasos, es pot veure que no és exactament cert. Fins i tot a temperatures i pressions normals, els gasos reals poden desviar-se lleugerament de l’comportament ideal. La desviació és molt més gran en condicions més extremes, com veurem a continuació:
Factors de compressió
Per a un gas ideal, PV = nRT. Es compleix que a l’dividir PV / nRT = 1.
Per als gasos reals això només és possible a pressions baixes (menors a 5 atmosferes). Analitzant la gràfica s’observa que la desviació es fa mes pronuncioada amb l’augment de la pressió. I augmentant la temperatura el gas pren un comportament proper a l’ideal.
En un gas real, a mesura que augmenta la pressió, el quocient entre PV / nRT augmenta a un nombre més gran que un, (PV / nRT > 1) distorsionant la idealitat. El mateix passa quan una temperatura disminueix, ja que el factor de compressibilitat torna a augmentar per sobre d’1 (PV / nRT > 1) a mesura que la temperatura s’acosta a un nombre menor .
Un gas ideal té un factor de compressibilitat igual a un, però el factor de compressibilitat per a un gas real pot variar enormement d’aquest número. Els gràfics de sota mostren com varia això per al nitrogen a mesura que vostè canvia la temperatura i la pressió.
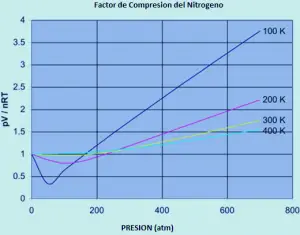
Si el nitrogen fos un gas ideal en totes les condicions de temperatura i pressió, cadascuna d’aquestes corbes seria una línia recta horitzontal que mostraria un factor de compressió de 1. (és clar que això no és veritat òbviament) .
a tenir en compte
a pressions baixes d’aproximadament una mica menys d’1 atmosfera, el factor de compressió s’aproxima a 1. el nitrogen s’aproxima a l’comportament ideal a pressions ordinàries . a El comportament no ideal empitjora a temperatures més baixes. Per a temperatures de 300 o 400 K, el factor de compressió s’aproxima a 1 en un ampli rang de pressions. El nitrogen es torna més ideal en un rang de pressió més gran a mesura que augmenta la temperatura. A El comportament no ideal empitjora a pressions més altes.
Hi ha d’haver al menys un efecte que faci que la relació PV / nRT sigui massa baixa, especialment a baixes temperatures. I ha d’haver al menys un efecte que faci que augmenti massa a mesura que augmenta la pressió.
Es manifesta el mateix comportament amb altres gasos?
El següent gràfic es mostra com els factors de compressió varien amb la pressió per a una varietat de gasos a una temperatura fixa de 273K.
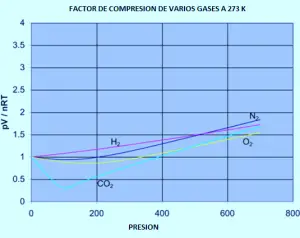
Si hagués de refer el conjunt de les gràfiques originals de nitrogen (a temperatures variables) per a qualsevol d’aquests altres gasos, trobaria que cada un d’ells produirà un conjunt de corbes similars a les de l’nitrogen. El que varia és la temperatura a la qual es produeixen les diferents formes gràfiques. Per exemple, si s’observa la gràfica de diòxid de carboni a 273 K (Gràfic anterior), es veu similar a la de nitrogen a 100 K de el primer conjunt de corbes, tot i que no augmenta tan pronunciadament a pressions més altes.
És fàcil dir que els gasos es tornen menys ideals a baixes temperatures, però el que compta com a baixa temperatura varia d’un gas a un altre. Com més a prop de la temperatura a la qual el gas es converteix en líquid (o, en el cas de l’diòxid de carboni, en un sòlid), més no ideal es torna el gas.
Què causa l’ comportament no ideal?
a les suposicions que fem sobre els gasos ideals, hi ha dues afirmacions que diuen coses que no poden ser veritables d’un gas real, i aquestes tenen un efecte tant en la pressió com en el volum .
el problema de l’volum: a La teoria cinètica suposa que, per a un gas ideal, el volum ocupat per les pròpies molècules és totalment insignificant en comparació amb el volum de l’recipient. Per a un gas de veritat (real), aquesta suposició no és certa. Les pròpies molècules ocupen una part de l’espai en el contenidor. L’espai en el contenidor disponible perquè les coses es moguin és menor que el volum mesurat de l’contenidor.
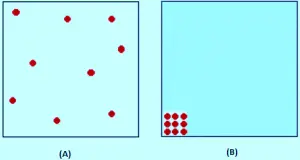
A la imatge (A) la teoria cinètica assumeix que tot aquest espai està disponible perquè les molècules es moguin dins. Però en realitat com es veu en la imatge (B), només aquesta quantitat d’espai està disponible, perquè la resta de l’volum és ocupat per les pròpies molècules.
Si la pressió és baixa, el volum ocupat per les molècules reals és insignificant en comparació amb el volum total de l’recipient.Però a mesura que el gas es comprimeix, la proporció de l’volum total que les pròpies molècules ocupen augmenta cada vegada més. Imagina que estàs comprimint tant el gas que les molècules es toquen entre si. En aquest punt el volum disponible perquè les molècules es moguin és zero.
Suposem que a una pressió elevada el volum de l’recipient és 1000 cm3, però suposant que les molècules ocupin fins a 100 cm3 d’ell.
L’equació de gas ideal es va elaborar fent càlculs basats en les hipòtesis de les teòriques cinètiques. Se suposa que V en PV és el volum disponible perquè les molècules es puguin moure lliurement, però en aquest cas només seria de 900 cm3, no de 1000 cm3.
Si calculem el factor de compressió, PV / nRT, posant el volum total de l’contenidor en la fórmula, el valor que obtindrem com a resultat sera mes alta del que hauria de ser (ja que el veritable volum hauria de ser 900 cm3).
Per a un gas real com el nitrogen, observeu com el factor de compressió tendeix a augmentar amb la pressió, mentre que per a un gas ideal, el factor de compressió seria d’1 a qualsevol valor de pressió.

el valor de el factor de compressió és massa alt a altes pressions per a un gas real. La raó d’això és que el volum mesurat que utilitzem en l’expressió PV / nRT és massa alt (recordem el cas anterior) i no tenim en compte el volum ocupat per les molècules. Aquest error es nota mes quan el gas es comprimeix.
El problema de la pressió: amor Una altra hipòtesi de la Teoria Cinètica per als gasos ideals és que no hi ha forces intermoleculars entre les molècules. Això està malament, ja que en els gasos reals això no és així. Si no hi ha forces intermoleculars seria impossible condensar el gas com líquid. Fins i tot l’heli, que posseeix la menor de totes les forces intermoleculars, pot convertir-se en un líquid si la temperatura és prou baixa.
Quin efecte tenen les forces intermoleculars? Per a una molècula de gas que es troba al centre de l’recipient, no hi haurà un efecte no (Imatge A). Les molècules s’atrauran fins a un punt on aquestes atraccions s’anul·lessin mútuament. Les atraccions exercida per la molècula de darrere, tendeixen a alentir, i seran cancel·lades per les atraccions de les molècules davant d’ella, tendint a accelerar-(ambdues atraccions es cancel·len).
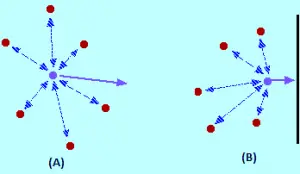
la molècula continués movent-se en la mateixa direcció a la mateixa velocitat, però quan aquesta per colpejar el contenidor passa el següent: a el no haver molècules davant d’ell, ja no es produeix el cancelamiento de les atraccions intermoleculars. Per tant, la molècula comença a disminuir la seva velocitat just abans de colpejar amb la paret de l’recipient (Imatge B). En conseqüència xocarà amb la paret amb menys força i menys pressió.
L’efecte general d’això és la culpable que la pressió sigui menor del que seria si el gas fos ideal. Això vol dir que si es col·loca la pressió mesura en l’expressió PV / nRT, el valor de el factor de compressió serà menor que si el gas fos ideal. Aquesta és la raó per la qual, en algunes condicions, els gràfics dels factors de compressió estan per sota de la valor ideal de 1. Vegem una altra vegada l’exemple de l’Nitrogen (Si ja ho se, t’has cansat de la gràfica jaja).

Aquest efecte és més important a baixes temperatures. Per què? A temperatures baixes, les molècules es mouen més lentament. A temperatures més altes, on les molècules es mouen molt més ràpid, qualsevol petit retrocés de la molècula cap al centre de el gas tot just es notarà. A altes temperatures, l’efecte de les forces intermoleculars és certament insignificant ja que les molècules escapen de les interaccions.
I hi ha un efecte final pel que fa a les forces intermoleculars, que està lleugerament més ocult. A mesura que augmenta la pressió, les molècules es troben mes juntes. Si estan més a prop, les forces intermoleculars seran més importants.
Quin és el gas més ideal?
a Hauríem buscar un gas les molècules siguin les més petites possibles, i on les forces intermoleculars siguin molt baixes. Aquest gas seria l’heli. Una molècula d’heli té en un sol àtom que és molt petit, i les forces de dispersió Van der Waals són molt baixes.
A l’igual que l’heli, una molècula d’hidrogen també té dos electrons, per la qual que les forces intermoleculars seran petites (però no tan petites com l’heli). En la molècula d’hidrogen, vostè té dos àtoms sobre els quals pot distribuir les càrregues.A mesura que les molècules es fan més grans, llavors les forces de dispersió augmentaran, i vostè pot obtenir altres forces intermoleculars com ara atraccions dipol-dipol. Els gasos fets de molècules com aquestes seran molt menys ideals.
L’equació van der Waals
Hi ha un gran nombre d’equacions que poden descriure com actuen els gasos reals, però per fer-ho simple , els químics s’adhereixen a l’equació Van der Waals perquè és la més fàcil de descriure com actuen els gasos:
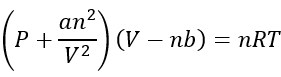
p és la pressió en atmosferes (atm) del V és el volum en litres (l) Anuncio n és el nombre de mols (mol) Respondre a és només una constant de proporcionalitat a b també és una constant de proporcionalitat
Tingues en compte que és molt similar a l’equació de gas ideal, però corregeix algunes coses.
el costat dret de l’equació és exactament el mateix que l’equació de gas ideal. Només canvia pel que fa a la pressió i el volum per donar compte de les coses pel que fa a les forces intermoleculars i el volum de molècules de gas.
Al costat esquerre explica una menor pressió que el d’un gas ideal, ja que té en compte les correccions que ocorren quan les molècules suavitzen l’impacte de les altres molècules a partir de les interaccions intermoleculars.