intersecție
SEAN \ (S \) și \ (T \) SEAN \ (S \) și \ (T \) SEAN \ (S \) și \ (t \) V \). Definim intersecția după cum urmează:
\ ({v \ în v \; ; \; V \ în t} \} \; \) Intersecția subspațiului
proprietate
\ (S \ Cap T \) este subspațiul \ (V \)
Demonstrație
1. \ ({0_V} \ în S \ Wedge {0_V} \ în t \ dreapta {0_V} \ în s \ cap t \)
2. Luați în considerare \ (u, \; v \; \; · \)
este dedusă \ (u + \; v \; \ \; \)
3. Lăsăm cititorul de către cititor să demonstreze:
\
Exemplu 1
văzut subspcioșul de \ (\ matethbb {r} ^ 3} \ ): 15fa2e3f9 ” \
\
gase \ (s \ cap t \).
Rezoluție
Prin definiție \ (S \ Cap T \) este un set care va fi format de vectorii care aparțin \ (S \) și \ (t \). Adică acei vectori care satisfac ecuațiile \ (S \) și cele ale \ (T \):
iv id = „15fa2e3f9” \
este aproximativ O dreaptă definită ca intersecție a două avioane. O bază a dreptului este un vector de regizor.
geometric putem căuta directorul vectorial ca produs vector al vectorilor normali la avioane:
\
\
apoi \ (\ stânga \ \ \ \; \ stânga ({3, – 2,1} \ dreapta) \;} \ Dreapta \} \) este o bază de \ (s \ cap t \).
O altă modalitate de a rezolva este de a căuta soluția de sistem Soluție:
iv id = ” 15FAA2E3F9″> \ \
și apoi ajungem la \ (\ stânga \ \ \; \ stânga ( {3, – 2.1} \} \;} \ dreapta \} \} este o bază de \ (s \ cap T \).
Exemplul 2
Fii sub -Sites \ ({\ matethbb {r} ^ {2 × 2}} \):
iv id = „15fa2e3f9” \
\
gase \ (s \ cap t \).
Rezoluție
Intersecția subspațiului este formată din vectorii care verifică ecuațiile din subspațiunile menționate.
Ce trebuie să fie îndeplinită o matrice să aparțină \ (S \)?
\
Ce trebuie să fie îndeplinită o matrice să aparțină lui \ (t \)?
trebuie să fie capabilă să fie scrisă ca o combinație liniară din: \ (\ stânga {array} {* {20} {c}} 1 & 0 \\ 2 & 0 \ end {array}} \ dreapta) \)
Noi găsim ecuațiile subspațiului \ (t \):
15fa2e3f9 „15FAA2E3F9” „15FAA2E3F9E3F9” \ > \
Considerăm că matricele de \ (s \ capitime) trebuie să respecte ecuațiile de \ (S \) și cele ale \ (T \):
\
\
Apoi matricele de \ (S \ Cap T \) sunt formularul:
iv id = „15fa2e3f9” \
și o bază de \ (s \ capac T \) ro:
iv id = „15fa2e3f9” \
Există o metodă alternativă mai scurtă pentru a găsi o bază de \ (s \ c AP T \) fără a fi nevoie să obțineți ecuațiile de \ (t \), după cum vom vedea mai jos.
Noi scriem o matrice de \ (t \) ca o combinație liniară a vectorilor care generează Acesta:
dar în plus, ecuațiile de \ (s \) care stabilesc că ar trebui îndeplinite \ (c = b \). Apoi:
\
Prin urmare, o matrice de \ (S \ Cap T \) este:
\
\
Având în vedere \ (s, \; t \; \) subspacios de \ (V \), suma după cum urmează:
\ (s + t = \; \ {v {v = {v_1} + {v_2} \; cu \; \; {v_1} {v_2} \; {v_2} \ în t} \ \ P> proprietate: \ (S + T \) este un subspațiu spațial vectorial \ (V \).
Lăsăm demonstrația de către cititor.
Dacă știm seturile S și T generatoare, putem găsi generatoare sumă:
\ (s = gen {{{v_1}, {v_2}, \ Ldots, {v_Q}} \ dreapta \} \) și \ (t = gen \ stânga {{{w_1}, {w_2}, \ Ldots, {w_r}} \ dreapta \} \) \ (\; \; S + t = gen \ stânga {{{v_1}, {v_2}, \ Ldots {v_Q}, {w_1}, {W_2}, \ Ldots, {W_R}} \ dreapta \} \)
pentru a găsi suma este de obicei pentru a căuta bazele \ (s \) și \ (t \). Deoarece bazele sunt seturi de generare Li, dacă știm o bază a fiecărui subspacio, putem obține un set de generatoare set:
Având în vedere bazele:
\ ({b_s} = \ stânga \ {{v_1}, {v_2, \ ldots, {v_Q}} \ dreapta \} \) și \ ({b_t} = \ stânga {{{w_1}, {W_2}, \ ldots, {w_r}} \ dreapta \} \)
\ (\ stânga \ {{{ V_1}, \ ldots, {v_Q}, {w_1}, \ Ldots, {w_r}} \ dreapta \} \) Set Generator Set.
observare: un set de generator de sumă este astfel obținut, dar nu este întotdeauna liniar independent.
- Dacă sunteți Li, găsim o bază de Suma.
- Dacă este LD, putem extrage o bază din sumă prin eliminarea vectorilor „Soboran”.
Exemplu 1
Având în vedere următoarele subspațiuni \ (v = {\ matethbb {r} ^ 3} \):
iv id = „15FAA2E3F9” \ \
Suntem interesați să găsim \ (S + T \).
Să căutăm o bază de \ (s \). Pentru aceasta în ecuația clarifică o variabilă:
\
Acum am setat un vector generic:
\
15fa2e3f9″> \
Găsiți o bază de \ (t \). Pentru aceasta în ecuația am șterge o variabilă:
iv id = „15fa2e3f9” \
Acum am setat un vector generic:
\
apoi
iv id = „15fa2e3f9” \
\
Știm că toate set de mai mult de 3 vectori în \ (\ matethbbk {r} ^ 3} \) este dependentă liniar, deoarece dimensiunea \ (\ matethbbk {r} ^ 3 } \) RO 3. Cum putem extrage o bază din sumă?
Am putea pune împreună o matrice cu acești 4 vectori și am luat-o la forma pasului. Sau dacă nu, deoarece spațiul este \ (\ matethbb {r} ^ 3} \) putem gândi geometric:
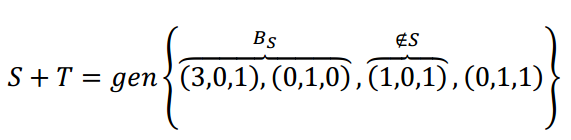
Ca \ (\ stânga ({1,0.1} \ dreapta) \) nu verifică ecuația planului S, primii 3 vectori nu sunt coplanari și, prin urmare, formează o bază de \ (\ Mathbb {r} ^ 3 \) . Putem șterge \ (\ Stânga ({0,1,1} \ dreapta) \) deoarece este o combinație liniară a bazei menționate.
Prin urmare: \ (b = \ stânga {\ stânga ({3.0 .1} \ dreapta), \ stânga ({0,1.0} \ dreapta), \ stânga ({1,0.1} dreapta)} \ dreapta \} \) este baza de \ (S + T \) și este baza de \ (\ matethbb {r} ^ 3 \).
În acest caz, cum ar fi \ (S + T \; \) este un subspațiu de \ ({r ^ 3} \) Dimensiune 3 , Putem afirma că:
iv id = „15fa2e3f9” \
Generalizare:
Exemplul 2
Având în vedere următoarele sub-pachete de \ (V = {\ Mathbb {r} ^ 4} \):
\
\
Găsirea bazei și dimensiunii \ ({s_1} + {s_2} \; \).
Rezoluție
\
\
\
iv id = „15fa2e3f9” \
Cum am văzut, a metoda de analiză dacă s Pe Li sau LD, constă în asamblarea unei matrice cu vectorii ca niște rânduri și o ia la forma pasului. Pentru comoditate vom plasa vectorii în ordinea următoare:
\ (\ la stânga {array} {20} {c}} 1 & {- 1} & 1 \\ 1 & 0 iv id = „26a2980253” {- 1} iv id = „26a2980253” 1 \\ 0 iv id = „26a2980253” 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ capătul {array}} \ dreapta) \)
iv id = „15fa2e3f9” \ (\ matethop \ la {f_2} {f_1}} \ stânga (\ incep {array} {* {20}} 1 & {- 1} iv id = „26A2980253” /div> 0 & 1 \\ 0 0 & 1 iv id = „26a2980253” {- 1} & 0 \\ 0 iv id = „26a2980253” 1 & 0 & 0 \\ 0 iv id = „26a2980253” 0 & 1 iv id = „26a2980253” 0 \ capătul {Array} } \ dreapta) \) /p>
\ (\ mathop \ to} – {f_2} {f_3} – {f_2}} \ stânga (\ begin {array} {* {20} {c} } 1 iv id = „26a2980253” {- 1} & 0 & 1 \\ 0 & 1 & {- 1} iv id = „26a2980253” 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \ capătul {array}} \ dreapta) \)
iv id = „15FAA2E3F9” \ (\ Mathop \ la {f_4}} {f_4} – {f_4}} {f_3}} \ stânga (\ incep {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 0 & 0 iv id = „26a2980253” 0 & 0 \ capătul {array}} \ dreapta) \)
arca matricea Lonaada are 3 rânduri Li (intervalul său este 3), apoi putem afirma că dimensiunea \ (S + T \) este 3.
ca ultimul rând a fost anulat, vectorul \ (\ stânga ({{{{0.0} \ dreapta) \) este o combinație liniară a celorlalte trei, prin urmare o bază de \ (s + t \) este: \ (b_ {s + t}} = \ stânga {{\ stânga ({1, – 1,0,1} →, \ stânga ({0,1,0, 0} → \ stânga ( {1.0, – 1.1} \ dreapta)} \ dreapta \} \).
Reamintim că rândurile matricei pasate reprezintă o altă bază a sumei:
divid id = „15FAA2E3F9 „> \
suma directă
cantitatea de două subspațiu este directă dacă și numai dacă intersecția de subepacios este vectorul zero.
Când suma este directă este scrisă:
\
exemple în \ ({\ rm {v} = {\ Mathbb {r} ^ 3} {{{\)
Apoi vom lua în considerare diferite sume de sumă de subspațiuni în \ (\ matethbbk {r} ^ 3} \ ).
Două drepte
Un posibil caz de suma a două subspcioși în \ (\ Mathbb {r} ^ 3} \) este cea din două drepte drepte care sunt tăiate :
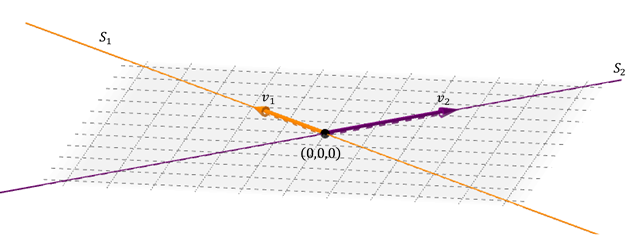
L. OS Două vectori directi Li generează o hartă: ceea ce conține ambele drepte. Suma este directă deoarece intersecția dintre liniile este vectorul nul.
iv id = „15fa2e3f9” \
{S_1} \ opus {s_2} = s \) unde \ (s \) este planul care conține cele două linii
două avioane care sunt tăiate
un alt caz posibil de sumă de Două subspațiuni în \ (\ matethbb {r} ^ 3} \) este cel dublu de două desen:
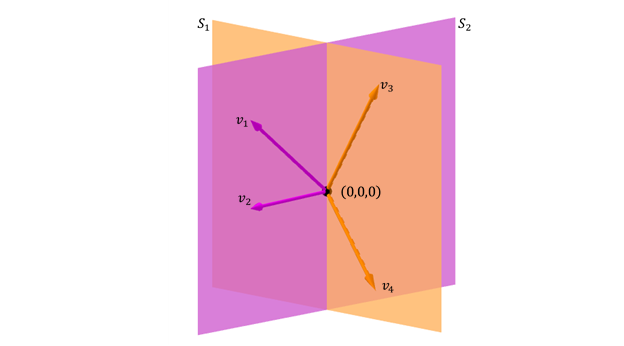
\}} = gen \; {v_1}, {v_2}, {v_3}} {v_3}} {v_3}} {v_3}} {v_3}} {v_3}} {v_3}} { Subspacios este \ (\ matethbb {r} ^ 3} \) dar nu este o sumă directă deoarece intersecția nu este vectorul zero:
iv id = „15fa2e3f9” \
un plan și un drept inclus în planul
un alt caz posibil de două subspațiu în \ (\ Mathbb {r} ^ 3} \) este cel al unui apartament și un drept inclus în avionul.
\
Același plan este obținut, iar suma nu este directă Deoarece intersecția nu este egală cu vectorul zero.
un plan și un drept nu este inclus în plan
un alt caz posibil de suma a două sub-apacios în \ ({{\ MATHBB {R} ^ 3} \) este cea a unui avion și a unei drepte care nu sunt incluse în plan. 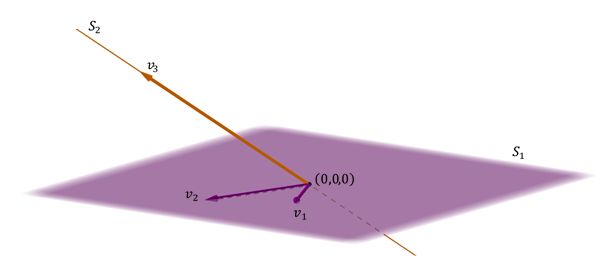
\
este generat \ (\ matethbb {r} ^ 3} \ ) Deoarece directorul vectorial al liniei nu se confruntă cu vectorii de avion și este, de asemenea, direct deoarece intersecția este vector nulă:
\
observare: în ultimul caz, Uniunea bazelor celor două subspațiuni formează o bază a întregului spațiu. În acest caz, fiecare vector al \ ({\ matethbb {r} ^ 3} \) poate fi exprimat într-un mod unic ca sumă a unui vector de \ (_1} \) și un altul din \ ({s_2} \).
Exercițiu pentru cititor 3
Dice \ ({s_1} = Gen \ stânga \ {{\ stânga ({1,2,1} dreapta), \ {stânga ({ 0.2,0} \ dreapta)} \ dreapta \} \) și \ ({s_2} = \ stânga {@ stânga ({x, y, z} \ dreapta): \; \; \; x + y = y – Kz = 0} \ dreapta \} \),
a) Găsiți valorile \ (k \) pentru care \ ({s_1} \ opus {s_1} = {\ Mathbb {r} ^ 3} \).
b) pentru \ (k = 0 \), verificați dacă \ (V = \ stânga ({3,2,2,2 \ dreapta) \) se poate exprima în un mod unic ca o sumă a unui vector \ ({v_1} \ în {s_1} \ în \ ({v_2} \ în {s_2} \ în {s_2} \ în {s_2} \).
Exercițiu pentru cititor 4
sunt sub-Appacios de \ ({\ Mathbb {r} ^ 4} \):
\ (s = gen \ stânga {\ stânga ({1,1,1, 1} \ dreapta), \ \ stânga ({0,1,0,1} \ dreapta)} \ dreapta \} \) și \ (t = \ stânga \ {{\ stânga ({x, y, z, t} → : \; xz + t = 0} \ dreapta \} \)
Care dintre următoarele afirmații este corectă? Justifica.
- \ (s \ opus t = {\ matethbb {r} ^ 4} \)
- \ (s + t = {\ matethbb {r} ^ 4} \)
- \ (s + t = w \; la stânga (w \ dreapta) = 3 \)
- \ (s \ oplus T = W \) și \ (Dim \ stânga (w \ dreapta) = 3 \)
Teorema dimensiunii sumului
Si \ ({ S_1} \) și \ ({s_2} \) sunt sub-spații ale unui spațiu vectorial \ (V \) (dimensiune finită), apoi:
în cazul în care suma este directă, cum ar fi {{s_1} → {_2} = \ stânga {{{{{0_V}} \ dreapta \} \ ), este:
\
exemplu
Având în vedere subspcioșii \ ({p_2} \):
\
\
Găsiți baze ale ambelor subspații și intersecția
rezoluție
găsim o bază de \ ({s_1} \):
iv id = „15fa2e3f9” \
Atunci sunt polinomii formularului:
iv id = „15fa2e3f9” \
apoi o bază de \ ({s_1} \) este:
\
găsim o bază de \ (s _2} \):
divid id = „15FAA2E3F9”> \
sunt polinomii formularului:
iv id = „15faa2e3f9” \
\
Pentru a căuta \ ({s_1} · \ cap {s_2} \) trebuie să luăm în considerare ecuațiile \ ({S_1} \) și, de asemenea, de \ (_2} \):
ivid id = „15fa2e3f9” \
Polinoamele vor fi în formularul:
\ \
Rețineți că, după cum știm dimensiunile \ (_1} \), \ ({s_2} {({s_2} {({s_1} · {s_2} · {s_2} ·), putem calcula dimensiunea \ ({s_1} + {s_2} \):
\
Dar singurul subspațiu al \ ({p_2} \) cu dimensiune 3 este \ ({p_2} \) . Apoi: \ ({s_1} + {s_2} = {p_2} \).
Exercițiu pentru cititor 5
Având în vedere subspcioșul de \ (\ matethbb {r} ^ {2 \ ori 2}} \):
iv id = „15fa2e3f9” \
\
a) găsiți baze de \ ({w_1} \) și \ ({w_2} \)
b) Obțineți \ ({w_1} → _2} \).
c) fără a găsi \ (w_1} + {w_2} \) Analizați validitatea următoarei afirmații:
\
d) Propuneți o bază de \ ({\ Mathbb {R} 2} \) formată de matricele simetrice și anti-immemétrice și exprimă matricea
\
ca o matrice simetrică plus un antishmetric.
produs intern
în prima unitate noi A văzut scalarul produsului între vectori și aplicațiile lor la geometrie. În această secțiune propunem generalizarea acestei operațiuni în alte spații vectoriale, definind noțiunea generală de produs intern din proprietățile produsului scalar.
Div>
Definiție: Un produs intern într-un spațiu vectorial real \ (V \) este o operație care atribuie fiecărui cuplu vector \ (U \) și \ (V \) de \ (V \) un număr real \ (U \; V \), cum ar fi următoarele proprietăți (pentru Toate vectorul \ (u, \; v, \; w \) de \ (V \) și tot scalar \ (\ alpha \)): 1. \ (U \ cdot v = v \ cdot u \)
2. \ (u \ cdot \ stânga ({v + w} \ dreapta) = \ stânga ({u \ cdot v} \ dreapta) + \ loft ({u \ cdot w} \ dreapta) \)
3. \ (α u \ cdot v = \ alpha \ stânga ({u \ cdot v} \ dreapta) \)
4. \ (Uu = 0 \; \; \; \; u = {0_v} \) /p>
este posibilă definirea diferitelor produse interne în orice spațiu vectorial (în timp ce aceste proprietăți sunt verificate). În subiectul nostru, vom lucra numai cu produsul intern canonic în \ (\ matethbb {r} ^ n} \), care este răspândirea produsului produs:
\ ({{x_1}, {x_2} \ ldots, {x_n}} \ dreapta). \ stânga ({y_1}, {y_2}, \ Ldots, {y_n}} \ dreapta) = {x_1} {y_1} + {x_2} {y_2} + \ ldots {x_n} {y_n} \} {y_n}} {
Această definiție ne permite să extindem conceptul de ortogonalitate la \ (\ matethbbk {r} ^ n} \):
\ (u \ bot v \; \; \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\, \; \ Mathbb {r} ^ 4} \):
ivid id = „15fa2e3f9”
\
\
ca \ (UV = 0 \) apoi \ (U \) și \ (V \) sunt ortogonale. \ (\; \)
complement ortogonal al unui subspațiu
Let \ (S \) subspațiu de \ (V \) (spațiu vectorial cu produs intern).
Completarea ortogonală a \ (s \), pe care o denunțăm ca \ (S \ Bo T} \), este setul vectorial al \ (V \) care este ortogonal pentru fiecare dintre vectori de \ (S \):
proprietate: \ ({s ^ \ bot} \) este un subspațiu de \ (V \).
1. \ ({0_V} \) aparține \ ({s \ bot} \) ca \ ({0_V} .w \; = \; 0 \) pentru tot \ (W \) de \ (S \)
2. Sean \ (u, v \ în {S ^ \ \ \} → 0 \ \; 0 \; \; \; Fortall w \ în s \ dreapta \ stânga ({U + V} \ dreapta) .w \; = \; uw \; + \; v.W \; = \; 0 \)
Prin urmare, \ (U + V \) este în \ ({s ^ \ bot} \)
3. Da \ (u ~ {s ^ \} → {^ ^ \ bot} \). De ce?
Exemplul 1
SEA \ (S = \ Stânga \ {\ Stânga ({x, Y, Z} \ dreapta) \ în {\ Mathbb {r} ^ 3 } \; | \; \; 2x + 3 și – z = 0} \ dreapta \} \). Găsiți \ ({s ^ \ bot} \).
rezoluție
Trebuie să căutăm \ (\ matethbb {r} ^ 3} \) care sunt perpendiculare pe toate Vectorii din acel avion.
Mai întâi căutăm o bază de \ (S \), de exemplu:
iv Id = „15FAA2E3F9”
\
Pentru a găsi complementul ortogonal, căutăm toți vectori \ (\ stânga ({x, y, z} \ dreapta) \) care sunt ortogonale la \ (\ stânga ({- 1 ,, 1.1} \ dreapta) \ ) YA \ (\ stânga ({0,1,3} \ dreapta) \).
Un sistem de ecuații care definesc suplimentul ortogonal: se obține
\
\
Ce este o bază subspace \ ({s ^ \ bot} \)?
\
Baza este un vector perpendicular pe plan \ (S \). Prin urmare, complementul ortogonal al unui avion care trece prin origine este linia perpendiculară care trece prin origine.
divid id = „15fa2e3f9”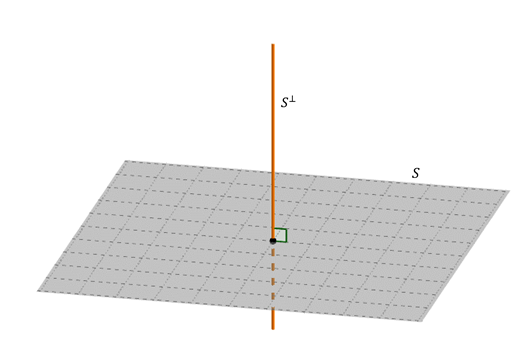
da \ (s \) este o linie care trece prin sursa: Care este suplimentul dvs. ortogonal?
Exercițiu pentru cititor 6
pentru a justifica procedura pe care o folosim pentru a găsi ecuațiile lui \ (^ \ \ bot} \), cerem să demonstreze următoarea proprietate:
sean \ (u, \; v, \ ; W \) vectori de \ (\ matethbb {r} ^ n} \).
si \ (w \) este ortogonal la \ (u \) deja \ (v \), apoi este ortogonală la orice combinație liniară de \ (U \) și \ (v \) ):
iv id = „15fa2e3f9” \
Halle Base și dimensiune a complementului ortogonal.
Rezoluție
Trebuie să căutăm vectorii de \ ({\ matethbb {r} ^ 4} \) care sunt ortogonale pentru vectorii \ (s \).
găsim o bază de \ (s \ ):
iv id = „15fa2e3f9” \ 15fa2e3f9 „> \
Acum căutăm \ ( \ stânga ({x_1}, {x_2}, {x_3}, {x_4}} {x_4}} {x_4}} {x_4}} {x_4}} {x_4}} {x_4}} {x_4}} {x_4}} \ dreapta) \ P> găsim ecuațiile care definesc \ (^ \ \ bot} \):
iv id = „15FAA2E3F9” \
Căutați o bază de \ (^ \ bot } \):
div id = „15FAA2E3F9”> \
Proprietăți ale complementului Ortogonal
SEA \ (V \) Un spațiu vectorial cu dimensiune fină, cu produs intern și BE \ (S \) Un subspațiu de \ (V \). Apoi sunt verificate următoarele proprietăți:
- \ ({{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{^ ~ BOT} = S \)
- \ ({v ^ \ {\ {\ {\ {{{{{{{{{{{{{{{{{{{{{{{{\; }} \ Bot}} {\; \ bot} = v \; \ bot} = v \; li>
- \ (s ^ ^ ^ \ bot} = \ stânga \ {{{0_V}} \ drept \) \ {{ Li>
- \ (s + {s \ \ bot} = v \)
Această ultimă proprietate înseamnă că orice vector \ (v \) se poate exprima ca o sumă de a Vector mai mult decât \ ({s ^ \ bot} \).
ilustrează cu un exemplu geometric de \ (\ matethbb {r} ^ 3} \):
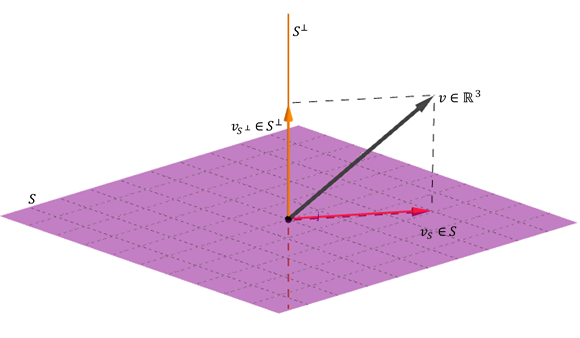
a proprietăților 3 și 4 este dedusă:
și, prin urmare:
legarea unei baze \ (S \) cu o bază de \ ({s ^ ^}} este baza de \ (v \). Acest lucru se aplică pentru a extinde o bază de \ (\; \) la o bază de \ (V \), așa cum se arată ca exemplul următor.
exemplu
mare \ (S = \ stânga \ {{\ stânga ({{x_1}, {x_2}, {x_3}, {x_4}} \ dreapta) \ în \ Mathbb {r} ^ 4 \;} + {x_1} + {x_1} – {x_2} + 3 {x_4} = 0 \}} \_1} = 0 \;} \ p>
Găsiți o bază de \ ( S \) și extindeți-l la o bază de \ (\ matethbb {r} ^ 4} \).
rezoluție
Căutăm un S, de exemplu:
\
ca \ (dim \ stânga (S / dreapta) = 2 \), putem anticipa că: \ (Dim ({s ^ \ Bot} \)) = 4-2 = 2
de la baza lui S, obținând ecuațiile \ (^ \ \ bot} \):
\
și găsim o bază de \ (^ \ \ \ bot} \), de exemplu:
\
apoi aderarea la bazele \ (s \) și \ ({s ^ \ bot} \) rezultate:
\ (b = \ stânga {{@ stânga ({1, – 2.0, – 1} →), \ stânga ({0.0,1,0} \ dreapta), \ stânga ({2,1,0} \ dreapta), \ stânga ({0,1.0, – 2} \ dreapta )} \ dreapta \} \) baza \ ({\ matethbb {r} ^ 4} \)
Exercițiu pentru cititor 7
zaruri Următoarele sub-Appacios \ ({\ Mathbb {r} ^ 4} \):
\ (S = \ stânga {{\ stânga ({x_1}, {x_2}, {x_3}, {x_4}} {x_4}} {x_1} = 0 {x_1} = 0 \; \; {x_2} + 2 {x_3} = 0 \;} \ dreapta \} \} \ \ dreapta \} \} \ dreapta \} \} \ dreapta \} \} \ „dreapta {{\ 2,3, k, 0} \ dreapta)} \ dreapta \} \)
Găsiți valorile \ (k \) pentru care \ (w = \; {s ^ \ bot} \).