Demonstrarea formulelor de zonă și volum utilizând integral

bun! În această intrare, formulele pe care le cunoaștem cu toții despre zona și volumul corpurilor cunoscute sub numele de cuburi, cercuri, sfere, piramide …

Pentru aceasta vor fi demonstrate, desigur, vom folosi integrarea numerică, Un instrument matematic esențial pentru orice tip de calcul care include o sumă infinitezimală de valori diferite.

pentru a putea înțelege perfect anumite calcule expuse pe care trebuie să le cunoașteți Cel puțin se integrează într-o variabilă și este foarte recomandat să vizitați acest articol: integral dublu și triplu. Modificări ale variabilelor

Formulele

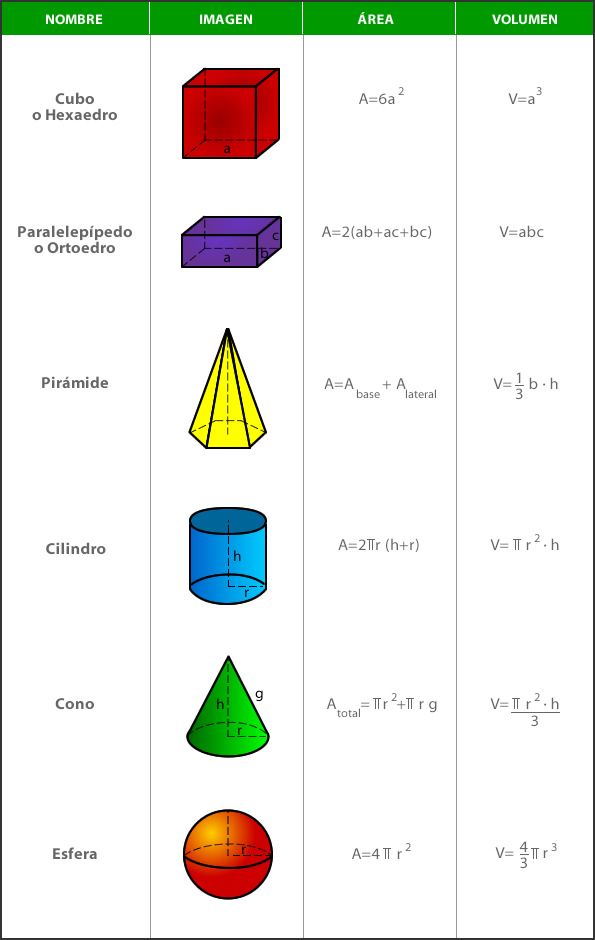
Pentru a calcula o zonă sau un volum, ceea ce se face este să calculezi integrale (simple, duble, triple, curbilinear, suprafață …) ale funcției constante F = 1 pe incintă a cărei dimensiuni Vrem să calculăm.

DIV ID = „E902317B43″>

Paralleplípedo

u toate acestea, ca prima utilitate de bază a integrării duble și triple, vom calcula volumul

volumul

incinta noastră de integrare este un paralelipiped de laturi A, B și C. Prin urmare, rămâne integrantă:

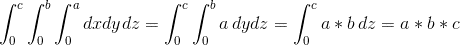
Demonstrarea formulelor de suprafață și volum utilizând integral 1

cerc

Toată lumea știe formulele sale:

$2 \ pi r$ și $\ pi r 2$ . Dar, cum deduceți?

În primul rând, trebuie să știm că dacă vrem să reprezentăm grafic o funcție de circumferință, nu poate fi reprezentată atât de ușor de forma și = f (x), deoarece nu este injectivă, Se spune că, pentru o valoare X, 2 valori apar și (formula generală pentru o rază Ry centrată pe originea coordonatelor este

<2} = r 2

. (În cazul doririi de a picta un cerc, se schimbă doar = prin < =). Prin urmare, se utilizează parametrizarea:

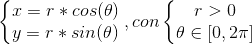
Demonstrarea formulelor de suprafață și a volumului prin integrele 2

a cărui determină Jacobiano, pentru schimbarea variabilelor este: R

Dacă doriți să aflați mai multe despre circumferință și cum obțineți formula într-un mod mai detaliat, acesta este articolul dvs.

Aici puteți juca un pic cu Ecuarea circumferinței: link către desmos

perimetru

r ECCTO este că „firul” care alcătuiește marginea exterioară a cercului. Prin urmare, curba parametrizată a firului menționat este:

divid id = „1417b485ef”>

calculul integrat curbilier pe funcția constantă f = 1 — >

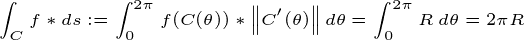
Area

Pentru a calcula Zona, este suficientă pentru a calcula integrale pe carcasa delimitată de circumferință. Pentru a facilita calculele pe care le trecem de la coordonatele carteziene (X, Y) la Polare (R,

$\ theta$ ) utilizând Jacobiano R pentru schimbarea variabilei. \ {} {0} {} {{^ {{} \ {0} ^ {2 \ {} ^ {2 \ {} ^ {2 \ {} ^ {2 \ Pi} R Drd {0} Ry Ry {0} Ry R Dr = 2 * \ Pi * \ \ frac {R2} {2} = \ Pi * R2

Sfera

Cazul sferei Formulele sale sunt oarecum mai necunoscute.

$\ frac {4} {3} * \ Pi * R 3$ pentru volum și $4 * \ pi * R 2$ pentru zona suprafeței sale.

Ca și în cerc, vom folosi alte coordonate, coordonatele sferice. Ecuația sferei în cartesiană este

parametrizarea en:

$\ stânga {matrice} x = r * sen (\ theta) * cos (\ phi) \\ y = r * Sen (\ theta) * Sen (\ phi) \\ z = R * cos (\ theta) \ capătul {matrice} \ dreapta$ , cu $\ stânga \ {\ începe {matrice} 0 \ leq r \ leq r \\ 0 \ leq \ PHI \ Leq 2 \ Leq \ Pi \ end {matrix} \ dreapta$

al cărui Jacobian este

$R 2 * Sen (\ theta)$

Aici puteți juca un pic cu ecuația sferei: introduceți geogebra 3D și lipiți acest lucru în editor: suprafață (R * Sen (U) * COS (V), R * SEN (U) * SEN (V) , R * COS (U), U, 0, PI, V, 0,2PI)

Area

Pentru a calcula zona, este suficient să calculați gama de călătorii Parametrizarea cu R = R.Noi calculăm integrale, făcând schimbarea variabilei cu Jacobian.

DIV ID = „E552138AF1″> \ {\ \ int_ {0} {\ Pi \ {0} {{\ PI} \ {0} ^ {2 \ Pi} R 2 * Sen (\ theta) D \ d \ phi = 2 * \ Pi * R 2 * \} Sen (\ theta) d \ theta = 4 * \ PI * R 2

Volume

Pentru volumul calculat integral întregii incinte

Folosind variabilele DR \ {0} ^ {{{\ \ {0} ^ {\ int_ {0} ^ {{\ { \ {} ^ {2 \ Pi} R 2 * Sen (\ theta) D \ theta d \ phi = 2 * \ {\ \ {0} ^ {\ pi} {} ^ {\ Pi { ° R 2 * SEN (\ theta) d \ theta dr \ dreapta

$\ dreapta 2 * \ {} \ pi} \ {0} ° R 2 * SEN (\ theta) d \ theta dr = \ frac {2} {3} * \ Pi * R 3 \ Int_ {0} ^ {\ Pi} Sen (\ theta) d \ theta = \ frac {4 } {3} * \ Pi * R 3$

Piramida

Modul de calculare a volumului unei piramide este identic cu cel al unui paralelipiped; Complicația este de a stabili limitele de integrare (incinta).

Logica de tragere, coordonatul Z va fi gratuit, variind de la 0 la h. Coordonatele XEY vor depinde de coordonatul Z privind valorile maxime pe care le iau, începând de la -B / 2 AB / 2 cel mult la bază și luând ca o singură valoare 0 când Z = H (vârf de piramidă). Pe baza acestei abordări, luăm limitele variabilelor:

$\ stânga {matrice} - \ frac {b} {2} * (1- \ frac {z } {H) \ leq x ≤ \ frac {b} {2} * (1- {2 {z} {h) {2} * (1- {2} * (1- \ frac {z} {h ) \ leq și \ leq {b} {2} * (1- \ frac {z} {h) \\ end {h) end {matrix} \ end$

Volum

Calculăm integral pe carcasa DXDYDZ

$v = \} \ int_ {} ^} \ int_ {} ^} \ int_ {- \ frac {b } {2} * (1- \ frac {z} {h)} ^ {h) {2} * (1- \ frac {z} {h)} \ {- \ frac {b} {2 } * (1- \ frac {z} {h)} ^ {h) {2} * (1- {2} d și dx = {{h} {0} ^ {h} b 2 * (1- \ frac {z} {h) 2 dz = \ dreapta>” height=”44″ width=”703″ style=”vertical-align: -16px;”> </p> <h2> Cone </h2> <p> Conul este foarte asemănător cu piramida. Cu toate acestea, trebuie să folosim coordonatele polare pentru a parametriza corect baza circulară. Vom folosi variabilele </p> <p> <img loading=$ . După o deducere similară cu piramida, am lăsat: $stânga \ \ începe {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r * (1- FRAC {z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ end {matrix} \ dreapta$

Volum

Calculăm integral pe carcasa Dixydz și Facem schimbarea variabilei la Polar cu Jacobiano R

IV id = „E5DE159290” V = \ ^ \ int_ {0} ^ \ int_ {0} ^ {{{ Z} {h)} \ int_ {0} ^ {2 \ Pi} R \ DZDRD \ Theta = \ Pi \ Int_ {0} ^ {h} R 2 * (1- CRAC {Z} {H) 2 = \ Dreapta

iv id = „735381bf7c” {H) = \ Pi * R 2 * 0 ^ {h} = \ PI * R ^ {2} * = \ Pi * R 2 * \ Frac {h} {3}

Care, ca Ne-am anticipat, la fel ca și piramida formula lui este

$zona \ de \ the \ base * \ frac {înălțime} {3}$

cilindru

Cilindrul este probabil cea mai intuitivă figură atunci când se calculează zona suprafeței și volumul acestuia. În ciuda faptului că este evident, vom arăta modul în care volumul dvs. ar putea fi calculat într-un mod integrat (fiind, în mod clar, zona de bază * înălțime), astfel încât funcționarea integrelor triple să fie mai bine înțeleasă.

Vom folosi Variabilele

$\ z, \ r \ y \ \ z, \ r \ y \ \ z, \ r \ y \ \ z, \ r \ y \ \ z, 0 \ leq z \ leq h \ \ leq r \ leq r \ \ Pi \ end {matrix} \ dreapta$

Volum

Calculăm integral despre carcasa DXDYDZ {0} ^ \ {{0} ^ \ {{0} ^ {r} {0} ^ {r} {0} ^ {r} { int_ {0} 2 r \ dzdrd \ theta = 2 \ p ^ int_ {0} ^ {h} \ int_ {0} ° r \ dzdr = \ dreapta

$\ dreaptarrow = \ Pi * R 2 * \ int_ {0} ^ h dz = \ pi * R 2 * h$

Demonstrarea formulelor și a volumului zonei prin intermediul integral

Formulele

Paralleplípedo

volumul

cerc

perimetru

Area

Sfera

Area

Volume

Piramida

Volum

Volum

cilindru

Volum

Lasă un răspuns Anulează răspunsul