a visão é o sentido pelo qual obtemos as maiores informações sobre o nosso ambiente . A interpretação do nosso cérebro, com base nas informações que recebe dos olhos, é fortemente influenciada pela experiência; Isso às vezes leva a erros de apreciação. Ao longo do tempo da sua vida, e especialmente nos primeiros idades, um indivíduo categorizado, generaliza e caracteriza os elementos do seu entorno para tomar decisões rapidamente. As pessoas que têm deficiências em seu senso de visão podem corrigir ou reduzir os defeitos disso por meio de lentes, isso é possível se falarmos sobre problemas de abordagem, por exemplo. Com o desenvolvimento na aquisição de imagens por meio de ferramentas tecnológicas, a necessidade de corrigir essas imagens também surgiu para que sua interpretação subseqüente seja verdadeira. Se um dispositivo de aquisição de imagens entregar imagens com defeitos de foco, essa deficiência pode ser corrigida adicionando lentes ao dispositivo. A perspectiva é um aspecto importante ao interpretar uma imagem, a fundação deste aspecto está na experiência, como é assim que aprendemos a estimar medidas, posições, velocidades, etc. Uma interpretação precisa da imagem obtida pode ser alcançada se as características do objeto lá contido são conhecidas pelo indivíduo que a analise. Há a importância das proporções da imagem, com relação à realidade, são congruentes. Também usamos a perspectiva para sugerir uma ideia para um indivíduo ou persuadi-lo, e lá encontramos coragem quando se trata de modificar as proporções dos elementos em uma imagem. Quando a imagem adquirida não corresponde ao que queremos visualizar, podemos fazer uma modificação da imagem para que seja mais conveniente.
modificar uma imagem, coordenar transformações dos pixels e modificações no brilho da imagem, este último é alcançado com técnicas de interpolação de brilho. Alterar as proporções da imagem pode ser compreendida com uma ação análoga: se tivermos uma superfície de gelo e expandirmos esta superfície com calor, obteremos uma superfície de vapor e haverá regiões vazias na dita superfície. O mesmo efeito acontece nas imagens e compensar esse defeito, são usadas técnicas de interpolação; Com essas técnicas, assumimos valores para lugares vazios para que a imagem seja apreciada uniforme, isso está relacionado à resolução da imagem. A maneira pela qual afetamos a geometria da imagem é baseada em técnicas de transformação geométrica. Se quisermos mover a imagem, alterar suas proporções de base e altura, girar ou deslizar, podemos realizar a transformação linear relacionada. Se você quiser mudar a geometria da imagem sem preservar o paralelismo entre as linhas opostas do contorno da imagem, podemos usar uma transformação bilineal ou uma transformação em perspectiva. Esta transformação usa 4 pontos de referência e 4 pontos de transformação para definir a função de transformação.


O objetivo desta prática é modificar uma imagem de altura “e” e base “x”. A imagem será modificada de dois pontos da imagem. Para formular O problema e descreve a solução proposta, uma imagem de exemplo será usada. É desejado modificar a imagem 2, para que o pixel marcado com um “X” vermelho seja selecionado e a posição que ela é desejada leva com um “ou” Roj ” A, para este caso. O ponto de referência “X” terá as coordenadas (PRX (1), pry (1)). O ponto de referência “ou” terá as coordenadas (PRX (2), pry (2)). O primeiro elemento da nomenclatura anterior corresponde à posição no eixo horizontal e no segundo elemento corresponde à posição no eixo vertical. Deve ser levado em conta que para localizar esses pontos O ponto de referência é no canto superior esquerdo da imagem.
A transformação linear será usada para modificar uma imagem com base na seleção de dois pixels de a imagem. Primeiro, o pixel “1” é selecionado e posteriormente o pixel “2”.A imagem mudará em relação a esses dois pontos de referência; Você quer mover o pixel “1” para a posição de pixel “2”, toda a imagem deve mudar para acomodar este novo ponto de referência. Dividindo a imagem em 16 células iguais (4×4), a solução é que cada célula muda para um formulário específico e todos esses novos formulários podem ser unidos para obter uma nova imagem das mesmas dimensões do original. O acima pode ser alcançado usando a transformação bilineal aplicada a cada célula.
A solução proposta é projetada para imagens formadas por uma única matriz, para que essa transformação não possa ser aplicada a imagens no formato RGB, por exemplo.
desenvolvimento de exercícios.
na imagem 2 é sobreposto uma malha azul, que deve mudar em relação à transformação desejada. Esta malha tem 3 linhas verticais e 3 linhas horizontais. A solução para o problema original é uma solução geral, portanto, apenas a imagem de exemplo é usada em determinados momentos da descrição para que a explicação seja mais clara.
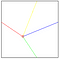
A primeira coisa que é feita é a localização de linhas de referência Acima, para a direita e à esquerda do ponto “X”. Eles são as linhas mais curtas do ponto “X” até as extremidades da imagem, como visto na imagem 3.A. As coordenadas do ponto “X” são (PRX (1), pry (1)).
Após localizar as linhas de referência, os pontos de corte de cada linha da malha com essas linhas de referência. É possível que as linhas de referência tenham pontos de corte com três, com dois, com uma ou nenhuma linha de malha. Abaixo estão os pontos de interseção para este caso na imagem 4.

são desenhados quatro linhas Referência Novo para representar gráfico a nova malha. O ponto Onde você se juntar a esta 4 novas linhas é o ponto “ou” cujas coordenadas são (PRX (2), pry (2)). Desta forma a parte amarela da parte do ponto (PRX (2), pry (2)) para O ponto (PRX (1), 1) O 1 corresponde à primeira linha de pixel da imagem, a parte azul da parte do PU Nto (PRX (2), pry (2)) a ponto (x, pry (1)) O X corresponde à última coluna de pixels da imagem, a parte vermelha da parte do ponto (PRX (2), pry (2 )) A ponto (1, pry (1)) O 1 corresponde à primeira coluna de pixel da imagem e da parte verde do ponto (PRX (2), PRRY (2)) ao ponto (PRX (1) , y) a coluna e corresponde à última linha de pixel da imagem, como mostrado na imagem 5.
Se você olhar, a localização dos pontos de interseção, na Figura 3, deve mudar em proporção para alterar o linha em que eles estão localizados. Depois de encontrar a proporção com a qual eles mudam e localiza-os em sua nova posição, obtemos o seguinte resultado: imagem 6. Na borda da imagem 6 pontos onde as linhas que compõem a malha são colocadas a partir desses indicadores e os novos pontos de interseção são traçou a nova malha. Na imagem 7 você pode ver isso. Os valores que se importam para nós na imagem 7 são aqueles que indicam os pontos de interseção das linhas descontínuas. 

Uniting estes pontos de interseção pode representar gráfico da nova malha. A nova malha é usada para referência visual, uma vez que fazer a transformação bilineal, só precisamos dos pontos de interseção.

A identificação da intersecção dos pontos é feita com equações retas, simplesmente o cruzamento das linhas que geram os pontos de interesse são calculados. Agora que os novos pontos da malha são conhecidos, podemos realizar a transformação bilineal de cada célula. Realizar a transformação para a célula onde a maior parte do rosto Lena for encontrado, o processo de transformação pode ser explicada. a transformação é realizado em uma região retangular que contém a nova região, ou seja, uma região retangular onde a região está contida delimitados por K5, K8, K9 e K6. Tomando como entrada os pontos que enquadram a cada célula e os novos pontos que realizamos a transformação bilineal. Após a transformação, obtemos a imagem 11 para a célula. 

Se fizermos a transformação de todas as células e sobrepor as regiões obtido o resultado da imagem 12.
Para evitar a sobreposição das regiões, como podemos ver na imagem 12, temos de cortar as regiões antes sobrepondo-los cada. Se cortar a célula de imagem 11 com o contorno K5, K8, K9 e K6 da imagem 9 obtemos o resultado da imagem 13.

Depois de corte e sobrepondo as regiões de corte, obtém-se o resultado da imagem.

Eu permiti que as bordas das regiões de sobreposição Para observar como a malha é afetado.
Resultado de diferentes pontos.

código MATLAB
Com o seguinte código você pode colocar até a etapa de transformação passo. Claro que você pode otimizá-lo.
clc; clear all; close all;im=imread(‘LenaMonoColor.bmp’);
=size(im);
a=round(x/4); %horizontal
b=round(y/4); %vertical
figure;imshow(im);
% =ginput(2);
% hold on;for k=0:5;
line(,);
line(,);
endim1=uint8(zeros(size(im)));
im2=uint8(zeros(size(im)));
im3=uint8(zeros(size(im)));
im4=uint8(zeros(size(im)));
im5=uint8(zeros(size(im)));
im6=uint8(zeros(size(im)));
im7=uint8(zeros(size(im)));
im8=uint8(zeros(size(im)));
im9=uint8(zeros(size(im)));
im10=uint8(zeros(size(im)));
im11=uint8(zeros(size(im)));
im12=uint8(zeros(size(im)));
im13=uint8(zeros(size(im)));
im14=uint8(zeros(size(im)));
im15=uint8(zeros(size(im)));
im16=uint8(zeros(size(im)));for xp=1:b;
for yp=1:a;
im1(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=a:a*2;
im2(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=2*a:3*a;
im3(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=3*a:4*a;
im4(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=1:a;
im5(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=a:2*a;
im6(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=2*a:3*a;
im7(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=3*a:4*a;
im8(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=1:a;
im9(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=a:2*a;
im10(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=2*a:3*a;
im11(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=3*a:4*a;
im12(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=1:a;
im13(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=a:2*a;
im14(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=2*a:3*a;
im15(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=3*a:4*a;
im16(xp,yp)=im(xp,yp);
end
endfigure,imshow(im1)
% figure,imshow(im2)
% figure,imshow(im3)
% figure,imshow(im4)
% figure,imshow(im5)
% figure,imshow(im6)
% figure,imshow(im7)
% figure,imshow(im8)
% figure,imshow(im9)
% figure,imshow(im10)
% figure,imshow(im11)
% figure,imshow(im12)
% figure,imshow(im13)
% figure,imshow(im14)
% figure,imshow(im15)
% figure,imshow(im16)
% line(px1,py1)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im21=uint8(zeros(size(im)));
for m=1:b+50;
for n=1:a+30;
im21(m,n)=im1(round(BP’*),round(AP’*));
end
end
figure, imshow(im21)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im22=uint8(zeros(size(im)));
for m=1:b+10;
for n=a:2*a;
im22(m,n)=im2(round(BP’*),round(AP’*));
end
end
figure, imshow(im22)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im25=uint8(zeros(size(im)));
for m=b+10:b*2;
for n=1:a+30;
im25(m,n)=im5(round(BP’*),round(AP’*));
end
end
figure, imshow(im25)X=’;
Y=’;
XP=’;
YP=’;
MP=;
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im26=uint8(zeros(size(im)));
for m=b:b*2;
for n=a:2*a;
im26(m,n)=im6(round(BP’*),round(AP’*));
end
end
figure, imshow(im26)im31=im21+im22+im3+im4+im25+im26+im7+im8+im9+im10+im11+im12+im13+im14+im15+im16;
figure, imshow(im31)
line(,)
line(,)
line(,)
line(,)
bilineal.m
Mostrando bilineal.m.