interseção
subespacios sean \ (s \) e \ (t \) do mesmo espaço de vetor \ ( V \). Definimos a interseção da seguinte forma:
\ (\ Cap t = \ left {{v \ in v \ ;: \; v \ in s \ ; \; \ Wedge \; \; v \ in t} \ direito \} \ \; \ \ \; \ \; \ \; \ \ \;
propriedade
\ (s \ cap t \) é subespaço de \ (v \)
demonstração
1. \ ({0_v} \ in s \ wedge {0_v} \ in t \ rightarrow {0_v} \ in s \ cap \)
2. Considere \ (u, \; v \; \; \; \)
\
\\]
\\]
de e é deduzido que \ (U + \; v \ \ \ \; \)
3. Deixamos o leitor pelo leitor para demonstrar:
\
Exemplo 1
visto os subspacios de \ ({\ mathbb {r} ^ 3} \ ):
\
\
encontrar \ (s \ cap t \).
Resolução
Por definição \ (s \ cap t \) é um conjunto que será formado pelos vetores que pertencem \ (s \) e \ (t . Isto é, aqueles vetores que satisfazem as equações de \ (s \) e os de \ (t \):
\
é sobre Um direito definido como interseção de dois planos. Uma base é um vetor de diretor.
Geometricamente, podemos pesquisar o diretor do vetor como o produto vetorial dos vetores normais para os aviões:
\
\
então \ (\ left \ \ \; \ left ({3, – 2,1} \ direito) \;} \ \} \} \) É uma base de \ (s \ cap t \).
Outra maneira de resolver, é procurar a solução de solução do sistema:
\
\
e, em seguida, chegamos a isso \ (\ left \ \ \; \ esquerda (esquerda {3, – 2.1} \ \ \ \ \ \} \} \} \) é uma base de \ (s \ cap \).
exemplo 2
ser o sub -sites de \ ({\ mathbb {r} ^ {2 × 2}} \):
\
\
localizar \ (s \ cap \).
Resolução
A intersecção do subespaço é formada pelos vetores que confirmam as equações dos referidos subespaços.
O que uma matriz tem que ser cumprida para pertencer a \ (s \)?
\
O que uma matriz tem que ser cumprida para pertencer a \ (t \)?
deve ser escrito como uma combinação linear de: \ (\ left ({\ begin {array} {* {} {*}} {c}} 1 & 0 \\ 2 & {- 1} \ end {matray}} \ direito) \; e \ left ({{{20} {} {c}} 1 & 0 \\ 1 & 0 \ end {matray}} \ direita)} \ \ \ p>
Encontramos as equações do subespaço \ (t \):
\
\
\
\
Agora consideramos que as matrizes de \ (s \ cap t \; \; \) devem cumprir as equações de \ (s \) e as de \ (t \):
\
\
Então as matrizes de \ (s \ cap t \) são o formulário:
\
e uma base de \ (s \ tap T \) PT:
\
Existe um método alternativo mais curto para encontrar uma base de \ (s \ c AP T \) Sem a necessidade de obter as equações de \ (t \), como veremos abaixo.
Escrevemos uma matriz de \ (t \) como uma combinação linear dos vetores que geram IT:
Mas, além disso, as equações de \ (s \) que estabelecem que \ (c = b \) devem ser cumpridas. Em seguida:
\
Portanto, uma matriz de \ (s \ cap t \) é:
\
sume de subpacies
dado \ (s, \; t \; \) subespacios de \ (v \), a soma da seguinte forma:
\ (s + t = \ left \ {{v \ in v \ ;: \; \; v = {v_1} + {v_2} \; \; \; \; \; \; {v_1} \ in s \ ;, \; \; {v_2} \ in t} \ rightht \) soma de subespacios
Propriedade: \ (S + T \) é um subespaço de espaço vetorial \ (v \).
deixamos a demonstração pelo leitor.
Se sabemos sets s e Geradores T, podemos encontrar geradores de soma:
\ (s = gene \ left {{{{{{{v_1}, {v_2}, {v_2}, {v_2}, {v_2} Ldots, {v_q} \ direito \} \) e \ (t = gene \ left {{{{{{w_1}, {w_2}, \ ldots, {w_r}} \ \; \} \) \ (\; \; S + t = gen \ left {{{v_1}, {v_2}, \ ldots {v_q}, {w_1}, {w_2}, \ ldots, {w_r}} \ right \}}} \ right \}}
Para encontrar a soma é usual para pesquisar as bases de \ (s \) e \ (t \). Como as bases são conjuntos de geração li, se soubermos uma base de cada subcacio, podemos obter um conjunto gerador de conjunto:
Dadas as bases:
\ ({b_s} = \ left \ {{{v_1}, {v_2, \ ldots, {v_q}} \ direito \}} e \ ({b_t} = \ left}, {W_2}, \ lDOTs, {w_r}} \ right \} \)
\ (\ left \ {{{{{{{{{{} V_1}, \ lDOTs, {v_q}, {w_1}, \ ldots, {w_r}} \ direito \} \) conjunto de gerador de soma.
Observação: Um conjunto gerador da soma é assim obtido, mas nem sempre é linearmente independente.
- Se você é li, encontramos uma base de a soma.
- Se for LD, podemos extrair de uma base a partir da soma, eliminando os vectores “Sobran”.
Exemplo 1
dadas as seguintes subespaços \ (V = {\ mathbb {R} ^ 3} \):
\
\
estamos interessados em encontrar \ (s + T \).
vamos buscar uma base de \ (s \). Para isso na equação, eliminamos uma variável:
\
Agora, definimos um vetor genérico:
\
\
Encontre uma base de \ (t \). Para isso na equação, eliminamos uma variável:
\
Agora, definimos um vetor genérico:
\
então
\
\
sabe-se que todos conjunto de mais do que 3 vectores em \ ({\ mathbb {R} ^ 3} \) é linearmente dependente, visto que a dimensão de \ ({\ mathbb {R} ^ 3 } \) EN 3. Como podemos extrair uma base a partir da soma?
poderíamos montar uma matriz com estes 4 vetores e levá-la à forma escalonada. Ou se não, como o espaço é \ ({\ mathbb {R} ^ 3} \) podemos pensar geometricamente:
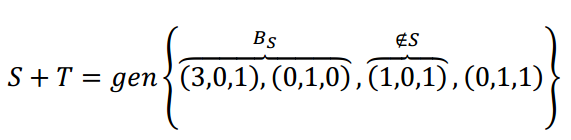
como \ (\ esquerda ({1,0.1} \ direito) \) não verifica a Equação do plano S, os primeiros 3 vectores não são coplanares e, por conseguinte, formam uma base de \ (\ mathbb {r} ^ 3 \) . Nós podemos excluir \ (\ esquerda ({0.1,1} \ direita) \), porque é uma combinação linear da referida base
, por conseguinte,:. \ (B = \ esquerda {{\ esquerda ({3,0 0,1} \ direito), \ esquerda ({0,1.0} \ direito), \ esquerda ({1,0.1} \ direito)} \ direita \} \) é de base \ (S + T \) e é de base de \ (\ mathbb {R} ^ 3 \)
neste caso, tal como \ (S + T \; \). é um subespaço de \ dimensão 3 ({R ^ 3} \) , podemos afirmar que:
\
generalizando:
\ (S \) Subspace \ (V \) e \ (\ Dim \ Esquerda (S \ right) = \ Dim \ Esquerda (V \ right) \ rightarrow S = V \)
Exemplo 2
dadas as seguintes sub-embalagens de \ (v = {\ mathbb {R} ^ 4} \):
\
\
Encontre base e dimensão do \ ({S_1} + {S_2} \; \).
resolução
\
\
\
\
\
Como vimos, um método para analisar se s Em Li ou LD, consiste em montar uma matriz com os vetores como linhas e levá-lo a sua forma escalonada. Por conveniência, colocaremos os vetores na seguinte ordem:
\ (\ left ({\ começo {array} {20} {c}} 1 & {- 1} & 0 & 1 \\ 1 & 0 & {- 1} & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ Mathop \ para {f_2} {f_1}} \ left ({\ begin {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array} } \ direito) \) ///p>
\ (\ mathop \ to} – {f_2} {F_3} – {f_2}} \ left ({\ begin {array} {* {20} {C} } 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ Mathop \ a {F_4 _4} {F_4} – {F_3}} \ left ({\ begin {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \ end {matray}} \ direito) \)
a matriz arca Lonada tem 3 li linhas (seu alcance é 3), então podemos afirmar que o tamanho de \ (s + t \) é 3.
À medida que a última linha foi anulado, o vector \ (\ esquerda ({{0.0,0} \ direita) \) é uma combinação linear dos outros três, portanto, uma base de \ (S + T \) é: \ ({B_ {S + T}} = \ esquerda {{\ esquerda ({1 – 1,0,1} →, \ esquerda ({0,1,0, 0} → \ esquerda ( {1.0, – 1.1} \ right)} \ right \} \)
Lembre-se que as linhas da composição da matriz intensificou outra base da soma:
\
soma direta
a quantidade de dois subespaço é direta se e somente se a intersecção de Subespacios é o vetor zero.
Quando a soma é direta está escrito:
\
Exemplos em \ ({\ rm {V} = {\ mathbb {R} ^ 3} \)
em seguida, vamos considerar diferentes somas de soma de subespaços em \ ({\ mathbb {R} ^ 3} \ ).
duas retas
Um possível processo de soma de dois subspacios em \ ({\ mathbb {R} ^ 3} \), é a uma das duas rectas rectas que são cortados :
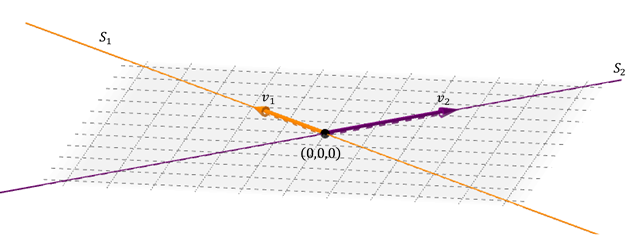
L. OS dois vetores retos geram um mapa: aquilo que contém ambas as retas. A soma é direta porque a interseção entre as linhas é o vetor nulo.
\
\ ( {S_1} \ OPUS {S_2} = s \) onde \ (s \) é o plano que contém as duas linhas
dois planos que são cortadas
Outra possível caso de sum de dois subespaços em \ ({\ mathbb {R} ^ 3} \) é o de dois desenho de dois desenho:
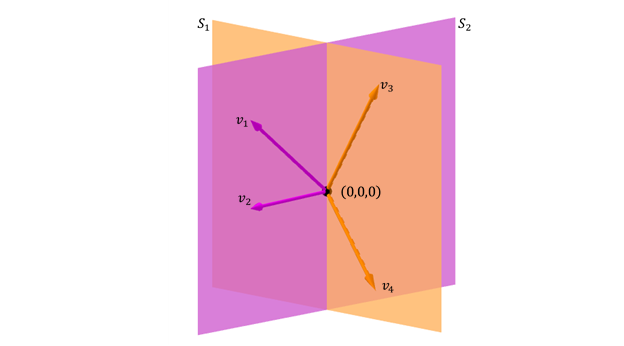
\}} = gene \ left \ {{\; {V 1}, {V_2}, {V_3}} \ rightHt \} \]
a soma do subspacios é \ ({\ mathbb {R} ^ 3} \) Mas não é soma direta porque o cruzamento não é o vetor de zero:
\
um plano e uma sequência incluída no
plano outra possível caso de dois subespaço em \ ({\ mathbb {r} ^ 3} \) é a de um plano e um linear incluído no o avião. 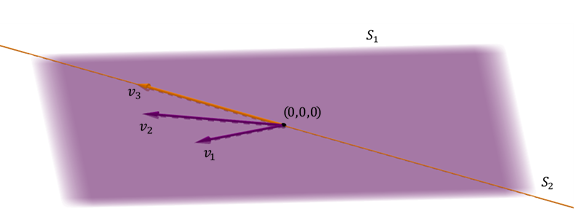
\
O mesmo plano é obtida, e a soma não é direta uma vez que a intersecção não é igual ao vector zero.
um plano e uma sequência não incluído no plano
Outra possível caso da soma das duas sub-appacios em \ ({\ mathbb {r} ^ 3} \) é a de um avião e um reto não incluído no plano.
\
é gerado \ ({\ mathbb {r} ^ 3} ) porque o diretor vector da linha não está lidando com os vetores de avião, e ele também é direta, pois o cruzamento é nulo vetor:
\
observação: no último caso, A união das bases dos dois subespaços forma uma base de todo o espaço. Neste caso, cada vetor de \ ({\ mathbb {r} ^ 3} \) pode ser expressa de uma forma única como soma de um vetor de \ (_1 \) e outro de \ ({s_2 \).
Exercício para leitor 3
dados \ ({s_1} = GEN \ left \ {{\ left ({1,2,1} \ right), \ \ left ({ 0.2,0} \ direito)} \ direita \} \) e \ ({S_2} = \ esquerda {\ esquerda ({x, y, z} \ direita): \; \; \; X + Y = Y – KZ = 0} \ right \} \),
a) encontrar os valores de \ (k \) para o qual \ ({S_1} \ opus {S_1} = {\ mathbb {R} ^ 3} \).
b) para \ (k = 0 \), verificação de que \ (V = \ esquerda ({3,2,2,2 \ direita) \) pode expressar-se em uma forma única como uma soma de um vetor \ ({V 1} \ in {S_1} \) e um dos \ ({V_2} \ in {S_2} \).
Exercício para o leitor 4
são as sub-appacios de \ ({\ mathbb {R} ^ 4} \):
\ (s = gene \ esquerda {\ esquerda ({1,1,1, 1} \ direito), \ \ esquerda ({0.1,0,1} \ direito)} \ direita \} \) e \ (t = \ esquerda \ {{\ esquerda ({x, y, z, t} → : \; \; \ ;, \; \; xz + t = 0} \ right \} \)
Qual das seguintes afirmações é correta? Justificar.
- \ (s \ opus t = {\ mathbb {r} ^ 4} \)
- \ (s + t = {\ mathbb {r} ^ 4} \)
- \ (s + t = w \; \; \; e \; \ di \ left (w \ direita) = 3 \)
- \ (s \ oplus T = w \) e \ (\ dim \ esquerda (w \ direita) = 3 \)
teorema da dimensão da soma
si \ ({ S_1} \) e \ ({s_2} \) são sub-espaços de um espaço vetorial \ (v \) (dimensão finita), então:
\
No caso específico que a soma é direta, como \ ({s_1} → {_2} = \ left {{{{{{0_v}} \ right \} \ ), é:
\
exemplo
Dado o subspacios \ ({p_2} \):
\
\
Encontre bases de ambos os subespaces e da interseção
Resolução
Nós encontramos uma base de \ ({s_1} \):
\
então são os polinômios do formulário:
\
Então uma base de \ ({s_1} \) é:
\
Nós encontramos uma base de \ ({s _2} \):
\
Então são os polinômios do formulário:
\
\
para search \ ({s_1} \ cap {s_2} \) devemos considerar que as equações de \ ({S_1} \) e também os de \ (_2} \):
\
Os polinomiais serão no formulário:
\
então:
\
Observe que, como sabemos as dimensões de \ (_1} \), \ ({s_2} \) e \ ({s_1} {s_2} {s_2} \), podemos calcular a dimensão de \ ({s_1} + {s_2} \):
\
mas o único subespaço de \ ({p_2} \) com dimensão 3 é \ ({p_2} \) . Então: \ ({S_1} + {s_2} = {p_2} \).
exercício para o leitor 5
Dado o subspacios de \ ({\ mathbb {r} ^ {2 \ vezes 2}} \):
\
\
a) encontrar bases de \ ({w_1} \) e \ ({w_2} \)
b) get \ ({w_1} → _2} \).
c) sem encontrar \ ({w_1} + {w_2} \) analisar a validade da seguinte afirmação:
\
d) Propor uma base de \ ({\ mathbb {r} 2} \) formado por matrizes simétricas e anti-immemétricas, e expresse a matriz
\
como uma matriz simétrica mais um antishymetric.
produto interno
na primeira unidade viu o produto escalar entre vetores e suas aplicações para a geometria. Nesta seção, propomos generalizar esta operação a outros espaços vetoriais, definindo a noção geral do produto interno das propriedades do produto escalar.
Definição: Um produto interno em um espaço real \ (V \) é uma operação que atribui a cada torque de vetor \ (u \) e \ (v \) de \ (v \) um número real \ (u \; v \), como as seguintes propriedades são verificadas (para Todo o vetor \ (u, \; v, \; w \) de \ (v \) e tudo escalar \ (\ alpha \)): 1. \ (U \ cdot v = v \ cdot u \)
2. \ (u \ cdot \ left ({v + w} \ à direita) = \ left ({u \ cdot v} \ direito) + \ loft ({u \ cdot w} \ direito) \)
3. \ (α u \ cdot v = \ alpha \ left ({u \ cdot v} \ direito) \)
4. \ (Uu ≥ \ GE 0 \; \; uu = 0 \; \; \ leftrightarrow \; \; \; \; u = {0_v} \) /p>
é possível definir diferentes produtos internos em qualquer espaço vetorial (enquanto essas propriedades forem verificadas). Em nosso assunto, só trabalharemos com o produto interno canônico em \ ({\ mathbb {r} ^ n} \), que é a propagação do produto da escala:
\ (\ left ({{x_1}, {x_2}} {x_n}} \ à direita). \ left ({{y_1}, {y_2}} \ ldots, {y_n}} \ à direita) = {x_1} {y_1} + {x_2} {y_2} + \ ldots {x_n} {y_n} \ (\ mathbb {r} ^ n \)
Esta definição nos permite estender o conceito de ortogonalidade a \ ({\ mathbb {r} ^ n}}}} ^ n} \):
\ (u \ bot v \; \ \ leftrightarrow \; \; uv = 0 \) condição de ortogonalidade
Exemplo
Deixe-nos executar o produto interno de \ ({ \ Mathbb {r} ^ 4} \):
\
\
como \ (uv = 0 \) então \ (u \) e \ (v \) são ortogonal. \ (\; \ (\; \ (\ h2> complemento ortogonal de um subespaço
Deixe \ (s \) subespaço de \ (v \) (espaço vetorial com produto interno).
O complemento ortogonal de \ (s \), que nós denotamos como \ ({s \ bo T} \), é o conjunto de vetores de \ (v \) que são ortogonais para cada um dos vetores de \ (s \):
propriedade: \ ({s ^ \ bot} \) é um subespaço de \ (v \).
1. \ ({0_v} \) pertence \ ({s \ bot} \) como \ ({0_v} .w \; = \; 0 \) para tudo \ (w \) de \ (s \)
2. Sean \ (U, v \ in {s ^ \ bot} → 0 \ Wedge vw \; = \; 0 \; \; \ fortall w \ in s \ rightarrow \ left ({u + v} \ direita) .w \; = \; uw \; + \; v.W \; = \; 0 \)
Portanto \ (u + v \) está in \ ({s ^ \ bot} \)
3. Sim \ (u ~ {s ^ \ bot} → {^ ^ \ bot} \). Por quê?
Exemplo 1
mar \ (s = \ left \ {\ left ({x, y, z} \ direito) \ in} {\ mathbb {r} ^ 3 } \; | \; 2x + 3 e – z = 0} \ direito \} \). Encontrar \ ({s ^ \ bot} \).
resolução
temos que procurar \ ({\ mathbb {r} ^ 3} \) que são perpendiculares a todos vetores desse plano.
Primeiro procuramos uma base de \ (s \), por exemplo:
\
Para encontrar o complemento ortogonal, procuramos todos os vetores \ (\ \ left ({x, y, z} \ direito) \) que são ortogonais \ (\ esquerda ({- 1 ,, 1.1} \ direita) ) YA \ (\ \ esquerda ({0,1,3 \ direito) \).
Um sistema de equações que definem o suplemento ortogonal:
\
O que é uma base de subpaço \ ({s ^ \ bot} \)?
\
A base é um vector perpendicular ao plano \ (s \). Portanto, o complemento ortogonal de um plano que passa pela origem é a linha perpendicular que passa pela origem.
Sim \ (s \) é uma linha que passa pela fonte: qual é o seu suplemento ortogonal?
exercício para o leitor 6
Para justificar o procedimento que usamos para encontrar as equações de \ (^ \ bot} \), pedimos que eles demonstram a seguinte propriedade:
Sean \ (U, \; v, \ ; W \) vetores de \ ({\ mathbb {r} ^ n}}} \>
si \ (w \) é ortogonal \ (u \) já \ (v \), então é ortogonal a qualquer combinação linear de \ (u \) e \ (v \).
Exemplo 2
dado próximo subespaço \ ({\ mathbb {r} ^ 4} \ ):
\
halle base e dimensão do complemento ortogonal.
Resolução
Temos que procurar os vetores de \ ({\ mathbb {r} ^ 4} \) que são ortogonais aos vetores \ (s \).
Nós encontramos uma base de \ (s \ ):
\
\
agora estamos procurando \ ( \ left ({{{x_1}, {x_2}, {x_3}, {x_3}} {x_4} \ \ direito) \) tal que:
\
Encontramos as equações que definem \ (^ \ bot} \):
\
procurar uma base de \ (^ \ bot } \):
\
\
Propriedades do complemento Ortogononal
Sea \ (v \) Um espaço vetorial de dimensão, com produto interno, e ser \ (s \) um subespaço de \ (v \). Em seguida, as seguintes propriedades são verificadas:
- {\ left ({^ \ bot}} \ direito) ^ \ bot} = s \)
- \ ({v} bot} = \ left \ {{\; {0_v} \;} \ \} \) e \ (\ left {{\; {0 {v \;} }} \ Direito \} {\; \ bot} = v \)
- \ (s ^ ^ ^ \ bot} = \ left} = \ left {{{0_v}} \ rightsht \) \)
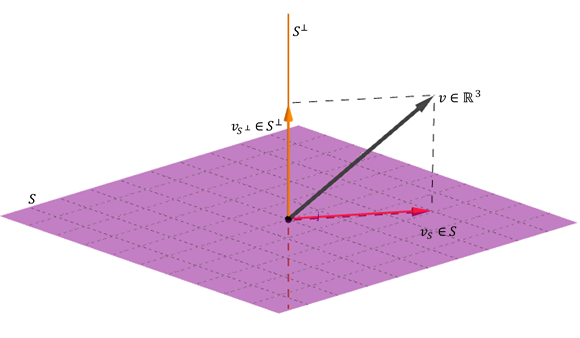
- \ (s + {s ^ \ bot} = v \)
it
esta última propriedade significa que qualquer vetor \ (v \) pode se expressar como uma soma de um vetor de mais diferente de \ ({s ^ \ bot} \).
ilustre com um exemplo geométrico de \ ({\ mathbb {r} ^ 3} \):
de propriedades 3 e 4 é deduzido:
e, portanto,
a ligação de uma base \ (s \) com uma base de \ ({s ^ \ bot} \) é base de \ (v \). Isso se aplica a estender uma base de \ (\; \) a uma base de \ (v \), conforme mostrado como o seguinte exemplo.
Exemplo
Sea \ (S = \ left \ {{\ esquerda ({{x_1}, {x_2}, {x_3}, {x_3}} \ direito) \ in {\ mathbb {r} ^ 4} \ ;: \; \ 4} \; {x_4} = 0 \; \; \; \; {x_1} – {x_2} + 3 {x_4} = 0 \;} \ direito \} \).
Encontre uma base de \ ( S \) e estenda-o a uma base de \ ({\ mathbb {r} ^ 4} \).
Resolução
Estamos à procura de um s, por exemplo:
\
como \ (DIM \ left (s \ direito) = 2 \), podemos antecipar que: \ (DIM ({S ^ \ Bot} \)) = 4-2 = 2
Na base de s, obtemos as equações de \ (^ \ bot} \):
\
e encontramos uma base de \ (^ \ bot} \), por exemplo:
\
Em seguida, juntando as bases de \ (s \) e \ ({s ^ \ bot} \) resultados:
\ (b = \ left {{\ esquerda ({1, – 2.0, – 1} →), \ \ left ({0.0,1,0 \ direito), \ left ({2,1.0.0} \ direito), \ left ({0.1.0, – 2} \ direito )} \ \ \ \ \} \) base de \ ({\ mathbb {r} ^ 4} \)
Exercício para o leitor 7
Dice os seguintes sub-appacios \ ({\ mathbb {r} ^ 4} \):
\ (S = \ left {{{{{x_1}, {x_2}, {x_3}, {x_3} \ logo) \; \; \; {x_1} = 0 \; \; \; \; {x_2} + 2 {x_3} = 0 \;} \ \} \) e \ (w = gene \ left {\ \ \; \ left ({1,0.0.0} \ logo ({ 2,3, k, 0} \ direito)} \} \} \)
Encontre os valores de \ (k \) para os quais \ (w = \; {s ^ \ bot} \).