… ou como a chance está do seu lado para obter mais nota
Você está fazendo um tipo de teste de teste, há quatro perguntas que você não sabe como responder e responder de forma errada você irá subtrair-lhe pontos. Se você decidir responder às quatro perguntas aleatoriamente, é mais provável que termine mais pontos do que se você não responder a nenhum. Essa afirmação parece correta, levando em conta que, se houver quatro perguntas com quatro opções de resposta, é lógico assumir que é mais provável que seja falhado três vezes e acertar um, se assumirmos que você atinge um ponto e falha permanece, no caso mais provável é que vamos ser o mesmo. Vale a pena uma rosa? A mesma coisa acontece com um número diferente de respostas aleatórias? Acontece que a matemática tem algo a dizer sobre isso …
Tipo de teste Os exames apresentam uma série de respostas a partir do qual você tem que escolher, normalmente, uma resposta correta. Em alguns testes de tipo de teste, há mais de uma resposta correta, às vezes as falhas subtrair pontos, pode haver respostas ponderadas ou um limite de perguntas que podem ser falhadas.
Posso aprovar se eu fizer um ensaio de tipo teste sem estudo
a idéia deste artigo é o de questões de estilo resposta: Can I aprovar, se eu faço um ensaio de tipo teste sem estudar? É a probabilidade do meu lado se eu respondi aleatoriamente? A mesma coisa acontece em qualquer tipo de teste? Qual é a diferença se as falhas subtrairem ou se não? Qual probabilidade eu tenho que aprovar se eu responder metade aleatória? E se eu tenho certeza se metade? E obter um notável? E um excelente?
Nós começamos no exame do tipo de teste mais simples, os sucessos adicionam, as falhas e as respostas não respondidas não afetam a nota.
Calculando a nota. ..
Nós definimos alguns nomes de variáveis:
n = total número de perguntas
a = número de sucessos
n = nota final
Se assumirmos que a nota é um número de 0 a 10 e o exame tem 10 questões do cálculo da nota é trivial . A nota obtida é igual ao número de perguntas bem-sucedidas:

… com um Baremo
Se o exame tem uma série de outros que o Barte da nota perguntas, para obter a nota final você tem que dividir o número de succes entre o número de perguntas e multiplicar por limite de borda superior.
para Exemplo: Se o baremo for de 0 a 10 e há 40 perguntas no exame, para tirar um 5 você tem que acertar 20 perguntas. Isto é, número de perguntas bem-sucedidas entre o número total: 20/40 = 0,5 e multiplicar o resultado pelo limite superior do baremo: 0,5 × 10 = 5.
generalização, para calcular uma nota em um tipo Teste de exame em que falhas não são subtraídos e temos um Barte:
bₛ = limite furo superior

Calculando probabilidades …
é bastante óbvio do que independentemente de saber se você sabe ou não as respostas, se as falhas não subtrair pontos, a melhor opção é para responder a tudo. Digamos que, em questão de pontos, você não tenha, literalmente, nada a perder.
Em qualquer caso, vamos formalizar o assunto com alguma matemática, quantas combinações de respostas são possíveis? E como depende desse número?
… com uma pergunta
O caso trivial é com uma única pergunta. Se tivermos 4 opções de resposta: A, B, C, D. Existem 4 possibilidades:

a probabilidade de que um evento ocorre é o número de possíveis eventos Entre as vezes o evento ocorre em questão. Nesse caso, existem 4 eventos possíveis, apenas 1 envolve atingir e 3 falhas:
A probabilidade de atingir responder aleatoriamente uma questão é de uma das quatro: 1/4 = 0,25. Normalmente, dizemos 25% de chance de bater.
A probabilidade de falha seria de três entre quatro: 3/4 = 0,75. Ou seja, é 75%.
Como vemos, neste caso, uma resposta aleatória tem tudo a perder. Também é interessante notar que, se adicionarmos as duas probabilidades, obtemos 100% desde, neste caso, há apenas dois resultados possíveis: para acertar ou falhar. Vamos ver que este não é o caso se houver mais de uma pergunta.
Em resumo …

… com duas perguntas (ou mais)
com duas perguntas que podem responder por exemplo: a no primeiro já no segundo, um no primeiro e b na segunda, b no primeira já no segundo … Estas são todas as combinações possíveis:

Estes são, em resumo todos os eventos possíveis respondendo duas perguntas. Eles são 16. Quatro vezes mais possibilidades do que com uma pergunta. This 4 vem do fato de que temos 4 opções de resposta, eo que acontece é que cada vez que adicionar uma questão que estamos multiplicando por 4 as combinações possíveis de respostas:
p₁ = número de opções de pergunta 1 | Pp = número de opções de pergunta 2
Cp = número de combinações de duas respostas
A fórmula seria:
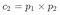
neste caso:
em geral, você só tem que multiplicar pelo número de opções, quantas vezes as perguntas existem :

Esta fórmula é fácil de simplificar, considerando que o número de opções é sempre o mesmo: p₁ = p₂ = p₃ = … = pₙ. Se definirmos:
n = número de perguntas
p = número de opções em cada questão
O número de combinações é calculado da seguinte forma:

neste caso, com p = 4 e n = 2:
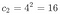
O próximo passo é para calcular as probabilidades. Neste caso, existem três eventos possíveis:
- sucesso todas as perguntas.
- Alcance uma pergunta (e falhe o outro).
- falha . perguntas
Tendo em conta todos os eventos possíveis, há apenas um caso em que todas as perguntas são aceitos, assumindo que as duas respostas corretas são a:

Portanto, a probabilidade de acertar as duas perguntas é 1/16 = 6,25%.
Generalizando , a probabilidade de ser todas dadas algumas perguntas número n é 1 entre todas as combinações possíveis de respostas, isto é:


A 4,25% de probabilidade já é bastante baixa, mas vamos ver como este percentual diminui drasticamente de acordo com Aumentamos o número de perguntas que respondemos aleatoriamente. Por exemplo, com 10 perguntas:

Como podemos ver, existem mais de um milhão de combinações possíveis, portanto, a probabilidade de acertar todas as respostas aleatórias é pequena.
… na verdade, é muito mais provável que toque na loteria.
Mas não somos tão ambiciosos, você não precisa acertar todos. Que probabilidade há para conseguir alguns? Assumindo novamente que as respostas certas são o A, estes são os tempos que nós batemos um respondendo a duas perguntas:

Observe que não destacamos aa porque eles são dois sucessos, nem um.
Nós temos 6 combinações possíveis que nos dão uma resposta bem sucedida, a probabilidade é mais nosso lado:

a probabilidade de levantar algo seria a soma dos dois anteriores, ou o mesmo, a possibilidade de obter tudo para as possibilidades de bater um:


não é ruim, de ter respondido tudo ao acaso.
A única coisa que permanece é saber a probabilidade de falhar tudo, e desde que é o único ou evento que nossos restos de probabilidade será o que está pronto para chegar a 100%, ou o que é o mesmo, o resto das combinações possíveis se subtrairmos os succes:

assim, a probabilidade de não ultrapassar cinqüenta por cento, então podemos apostar que certamente não irá adicionar pontos respondendo a duas perguntas aleatórias.
E assim seria a tabela resumida adicionando as chances com duas perguntas: