Demonstração de fórmulas de área e volume usando integrais

bom! Nesta entrada as fórmulas que todos sabemos sobre área e volume de corpos conhecidos como cubos, círculos, esferas, pirâmides …

Para isso será demonstrado, é claro, usaremos a integração numérica, Uma ferramenta matemática essencial para qualquer tipo de cálculo que inclua uma soma infinitesimal de valores diferentes.

Para ser capaz de compreender perfeitamente certos cálculos expostos que você tem que saber pelo menos integrar-se em uma variável, e é altamente recomendável visitar este artigo: Integrais duplas e triplas. Mudanças de variáveis

tabela de conteúdo

as fórmulas

Para calcular uma área ou volume, o que é feito é calcular a integral (simples, duplo, triplo, curvilinear, superfície …) da função constante f = 1 no gabinete cujas dimensões Queremos calcular.

paralelepípedepio

empregando integrais para este corpo geométrico é equivalente a matar moscas ao canhão; No entanto, como a primeira utilidade básica de integrais duplas e triplas, vamos calcular seu volume

volume

Nosso gabinete de integração é um paralelepeito de lados A, B e C. Portanto, a integral permanece:

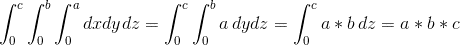
círculo

todos sabem que suas fórmulas:

$2 \ pi r$ e $\ PI R 2$ . Mas, como eles deduzem?

Primeiro de tudo, devemos saber que, se quisermos representar graficamente uma função de circunferência, não pode ser representada tão facilmente a partir do formulário e = f (x), pois não é injectivo, Está dizendo, por um valor X, aparecem 2 valores e (a fórmula geral para um raio Ry centrado na origem coordenada é

<2} = r 2

(no caso de querer pintar um círculo, basta mudar = por < =). Portanto, a parametrização é usada:

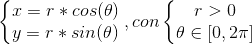
Demonstração de fórmulas e volume da área via integrais 2

cujo jacobiano determinante, para a mudança de variáveis é: R

Se você quiser saber mais sobre a circunferência e como você obtém sua fórmula de uma forma mais detalhada, este é o seu artigo

aqui você pode jogar um pouco com o equação da circunferência: link para Desmos

perímetro

o r Eccto é esse “fio” que compõe a borda externa do círculo. Portanto, a curva parametrizada do fio dito é:

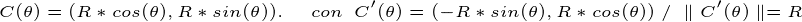
Demonstração de fórmulas de área e volume por integrais 3

Calculando a integral curvilínea na função constante f = 1 — >

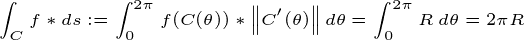
Área

para calcular A área, basta calcular a integral no recinto delimitado pela circunferência. Para facilitar os cálculos que passamos das coordenadas cartesianas (X, Y) para Polares (R,

$\ theta$ ) usando o Jacobiano R para a mudança de variável. $\ int_ {s} dxdy = \ int_ {0} ^ {} \ int_ {0} ^ {2 \ pi} r drd \ theta = 2 * \ pi \ int_ {0} ry r dr = 2 * \ pi * \ frac {R 2} {2} = \ pi * R 2$

esfera

o caso da esfera suas fórmulas são um pouco mais desconhecidas.

$\ frac {4} {3} * \ pi * r 3$ para volume e $4 * \ pi * R 2$ Para a área de sua superfície.

Como com o círculo, usaremos outras coordenadas, as coordenadas esféricas. A equação da esfera na Cartesiana é

a parametrização PT:

\ left \ {\ começo {matrix} x = r * sen (\ theta) * cos (\ phi) \\ y = r * sen (\ teta) * sen (\ phi) \\ z = R * cos (\ theta) \ end {matrix} \ direita

, com $\ left \ {\ begin {matrix} 0 \ leq r \ leq r \\ 0 \ leq \ Phi \ leq 2 \ leq \ pi \ end {matrix} \ direita$

cujo jacobiano é

$r 2 * sen (\ theta)$

Aqui você pode jogar um pouco com a equação da esfera: Digite geogebra 3D e cole isto no editor: superfície (r * sen (u) * cos (v), r * sen (v) * sen (v) , R * cos (u), u, 0, pi, v, 0,2pi)

Área

Para calcular a área, basta calcular o intervalo de a parametrização com r = r.Calculamos a integral, tornando a mudança de variável com o jacobiano.

$\ int \ int_ {s} dxdy = \ int_ {0} ^ {\ pi} \ int_ {0} ^ {2 \ PI} R2 * sen (\ theta) d \ d \ phi = 2 * \ pi * r 2 * \ int_ {0} ^ {\ pi} sen (\ teta) d \ theta = 4 * \ \ \ PI * R 2$

volume

para o volume calculamos a integral de todo o gabinete

usando as variáveis $Drd \ THETA D \ PHI$ $\ righttarrow 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ° R2 * sen (\ teta) d \ theta dr = \ frac {2} {3} * {0} \ pi * r 3 \ int_ {0} ^ {\ pi} sen (\ theta) d \ theta = \ frac {4 4 } {3} * \ pi * r 3$

pirâmide

A maneira de calcular o volume de uma pirâmide é idêntica à de um paralelepiped; A complicação é estabelecer os limites de integração (o gabinete).

tração lógica, a coordenada Z será livre, variando de 0 a h. As coordenadas Xey dependerão da coordenada Z em relação aos valores máximos que levam, a partir de -b / 2 AB / 2 no máximo na base e tomando como um valor único 0 quando o Z = H (pico pirâmide). Com base nessa abordagem, assumimos os limites das variáveis:

volume

calculamos a integral no gabinete dxdy

$v = \ iiint_ {v} dxdydz = \ int_ {0} ^} \ int_ {- \ frac {b } {2} * (1- \ frac {z} {h)} ^ \ frac {b} {2} * (1- \ frac {z}}}} {\ frac {2 } * (1- \ frac {z} {h)} ^ \ frac {b} {2} * (1- \ frac {z} {h)} d e dx = \ int_ {0} ^ {0} b 2 * (1- \ FRAC {z} {h) 2 dz = \ dightarrow$

cone

O cone é muito semelhante à pirâmide. No entanto, devemos usar coordenadas polares para parametrizar corretamente a base circular. Vamos usar as variáveis

$\ z, \ r \ \ theta$ . Após uma dedução semelhante à pirâmide, deixamos: $\ left \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r * (1- \ frac {z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ end {matrix} \ direito$

volume

calculamos a integral no gabinete dixydz e Fazemos a mudança de variável para polar com Jacobiano R

$v = \ iiint_ {v} dxdydz = \ int_ {0} ^ \ int_ {0} q (1- \ frac { Z} {h)} \ int_ {0} 2 r \ dzdrd \ teta = \ pi \ int_ {0} ^ {0} ^ {h} R2 * (1- \ crac {z} {h) 2 = \ righttarrow$ $= \ righttarrow \ pi * r 2 \ int_ {0} ^ ^ {h} (1+ \ frac {z 2} {h 2} - \ frac {2z} {h) = \ pi * r 2 * 0 ^ {h} = \ pi * r ^ {2} * = \ pi * r 2 * \ frac {h} {3}$

que, como nós antecipamos, apenas Como a pirâmide, sua fórmula é

$Área \ De \ The \ Base * \ Frac {Altura} {3}$

cilindro

o O cilindro é talvez a figura mais intuitiva ao calcular a área da superfície e seu volume. Apesar de ser óbvio, mostraremos como seu volume poderia ser calculado de forma integral (sendo, claramente, área de base * altura) para que a operação de integrais triplas seja melhor compreendida.

Vamos usar as variáveis

$\ z, \ r \ z, \ r \ \ \ \ theta$ tais: $\ left \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r \\ \ pi \ end {matrix} \ direito$

volume

calculamos a integral sobre o gabinete dxdydz e tornar a mudança de variável para polar com jacobiano r

$\ righttarrow = \ pi * r 2 * \ int_ {0 } ^ h dz = \ pi * r 2 * h$

Demonstração de fórmulas de área e volume via integrais

as fórmulas

paralelepípedepio

volume

círculo

perímetro

Área

esfera

Área

volume

pirâmide

volume

cone

volume

cilindro

volume

Deixe uma resposta Cancelar resposta