Intersection
Sean \ (s \) et \ (t \) sous-facespios du même espace de vecteur \ ( V \). Nous définissons l’intersection comme suit:
\ (\ cap t = \ left {{v \ dans v \ ;: \; V \ s dans \ ; \; \ wedge \; \; V \ T} \ right \} \; \) intersection de sous – espace
propriété
\ (s \ cap t \) est sous l’espace de \ (v \)
démonstration
1. \ ({0_v} \ in s \ wedge {0_v} \ in t \ RightARrow {0_v} \ en s \ cap t \)
2. Considérons \ (U, \; V \; \ dans \; · \)
\
\\]
\\]
et il est déduit que \ (u + \ \; v \ \ \ \; \)
3. Nous laissons le lecteur par le lecteur à démontrer:
\
Exemple 1
Vu le subspacios de \ ({\ mathbb {R} ^ 3} \ ):
\
\
trouver \ (cap \ s t \).
Résolution
par définition \ (s \ cap T \) est un ensemble qui sera formé par les vecteurs appartenant à \ (s \) et \ (t \). C’est-à-dire que ces vecteurs qui satisfont les équations de \ (s \) et celles de \ (t \):
\
est à propos de Une ligne droite définie comme intersection de deux avions. Une base de la droite est un vecteur de réalisateur.
géométriquement Nous pouvons rechercher le réalisateur de vecteur comme produit vectoriel des vecteurs normaux des avions:
\
\
alors \ (\ left \ \ \; \ left ({3, – 2,1} \ right) \;} \ Droite \} \) est une base de \ (s \ cap t \).
Une autre façon de résoudre est de rechercher la solution System Solution:
\
\
et puis on arrive à ce que \ (\ left \ \ \; \ left ( {3, – 2,1} \ right) \;.} \ right \} \) est une base de \ (S \ cap t \)
Exemple 2
être sous -Sites de \ ({\ mathbb {r} ^ {2 × 2}} \):
\
\
trouver \ (cap t de s \).
résolution
L’intersection de sous – espace est formé par les vecteurs qui vérifient les équations desdites sous-espaces.
Qu’est-ce que une matrice doit être remplie d’appartenir à \ (s \)?
\
Qu’est-ce que une matrice doit être remplie d’appartenir à \ (t \)?
doit pouvoir être écrit comme une combinaison linéaire de: \ (\ left ({\ begin {array} {* {20} {c}} 1 & 0 \\ 2 & {- 1} \ end {array}} \ right) \ et \ left ({{{20} {c}} 1 & \\ 0 1 & 0 \ end {array}} \ right) \)
On trouve les équations subspatiales \ (t \):
\
\
\
\
Nous considérons maintenant que les matrices de \ (S \ Cap t \; \ \) doivent être conformes aux équations de \ (s \) et celles de \ (t \):
\
qui est:
\
Ensuite , les matrices de \ (s \ cap t \) sont la forme:
\
et une base de \ (s \ Cap T \) fr:
\
Il y a une méthode alternative plus courte pour trouver une base de \ (s \ c AP T \) Sans la nécessité d’obtenir les équations de \ (t \), comme nous le verrons ci-dessous.
Nous écrivons une matrice de \ (t \) comme une combinaison linéaire des vecteurs qui génèrent il:
Mais en plus, les équations de \ (S \) qui établissent que \ (c = b \) doit être remplie. Puis:
\
Par conséquent, une matrice de \ (S de cap t \) est:
\
SUME dE SUBSPACIES
donnée \ (S, \; T \; \) Subespacios de \ (V \), la somme comme suit:
\ (S + t = \ left \ {{V \ dans V \ ;: \; \; V = {V_1} + {} V_2 \; \ ;, \; \; avec \; \; {V_1} \ dans l \ ;, \; \; {V_2} \ t} dans \ rightHt \) SOMME dE SUBSPACIOS
propriété:.. \ (S + T \) est un sous – espace espace vectoriel \ (V \)
nous quittons la démonstration par le lecteur
Si nous savons ensembles S et générateurs T, nous pouvons trouver des générateurs de somme:
\ (s = gène \ left {{{{{{{V_1}, {V_2}, \ ldots, {V_Q}} \ right \} \) et \ (t = gène \ left {{{{W_1}, {W_2}, \ ldots, {W_R}} \ right \} \) \ (\; \ rightarrow \; S + T = GEN \ left {{{V_1}, {V_2}, \ ldots {V_Q}, {W_1}, {W_2}, \ ldots, {W_R}} \ right \} \)
Pour trouver la somme est habituelle pour rechercher les bases de \ (s \) et \ (t \). Étant donné que les bases sont des ensembles de génération de LI, si nous connaissons une base de chaque sous-espacio, nous pouvons obtenir un ensemble de générateur de jeu:
donné les bases:
\ ({b_s} = \ left \ {{{V_1}, {V_2, \ ldots, {V_Q}} \ right \} \) et \ ({b_t} = \ left {{{W_1}, {W_2}, \ ldots, {W_R}} \ right \} \)
résultats:
\ (\ left \ {{{ V_1}, \ ldots, {v_q}, {w_1}, \ ldots, {w_r}} \ right \} \) SUM Generator SUM.
Observation: Un ensemble de générateurs de la somme est ainsi obtenu, mais il n’est pas toujours indépendant linéairement.
- Si vous êtes Li, nous trouvons une base de La somme.
- S’il s’agit de LD, nous pouvons extraire une base de la somme en éliminant les vecteurs « Sobran ».
Exemple 1
> Compte tenu des sous-espaces suivants \ (v = {\ mathbb {r} ^ 3} \):
\
\
Nous sommes intéressés par la recherche de \ (S + T \).
Recherche une base de \ (s \). Pour cela dans l’équation, nous effacons une variable:
\
Nous définissons un vecteur générique:
\
\
trouver une base de \ (t \). Pour cela dans l’équation, nous effacons une variable:
\
Nous définissons un vecteur générique:
\
alors
\
\
Nous savons que tout ensemble de plus de 3 vecteurs dans \ ({\ mathbb {r} ^ 3} \) dépend linéairement, depuis la dimension de \ (\ \ mathbb {r} ^ 3 } \) Fr 3. Comment pouvons-nous extraire une base de la somme?
Nous pourrions rassembler une matrice avec ces 4 vecteurs et le prendre à la forme étamée. Ou sinon, comme l’espace est \ ({\ mathbb {r} ^ 3} \), nous pouvons penser géométriquement:
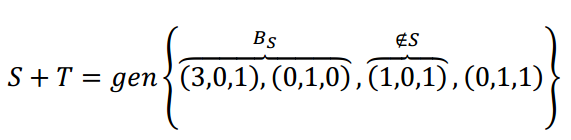
Comme \ (\ Gauche ({1,0,1} \ droite) \) ne vérifie pas l’équation du plan S, les 3 premiers vecteurs ne sont pas coplanar et forment donc une base de \ (\ mathbb {r} ^ 3 \ ^ 3 \) . Nous pouvons supprimer \ (\ gauche ({0,1,1} \ droite) \) car il s’agit d’une combinaison linéaire de ladite base.
Par conséquent: \ (b = \ gauche {{{{{{13. .1} \ droite), \ Gauche ({0,1.0} \ droite), \ gauche ({1,0,1} \ droite)} \ droite \} \) est la base de \ (s + t \) et est la base de \ (\ mathbb {r} ^ 3 \ \ \ \ \ \ \ \ \ \ \
dans ce cas, tel que \ (S + T \; \) est un sous-espace de \ ({R ^ 3} \) DIMENSION 3 , nous pouvons affirmer que:
\
Généralisation:
Exemple 2
Compte tenu des sous-paquets suivants de \ (v = {\ mathbb {r} ^ 4} \):
\
\
trouver la base et la dimension de \ ({s_1} + {s_2} \; \).
Résolution
\
\ \
\
\
Comment nous avons vu, Méthode d’analyse si s Sur LI ou LD, il consiste à assembler une matrice avec les vecteurs comme des lignes et de la prendre à sa forme étamée. Pour plus de commodité, nous allons placer les vecteurs dans l’ordre suivant:
\ (\ \ \ commencez {array} {20} {C}} 1 & {- 1} & 0
0 \\ 0 & 0 & 1 & 0 \ fin {array}} \ droite) \)
\ (\ mathop \ à {f_2} {f_1}} \ gone ({\ commencez {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 1
\ (\ mathop \ to} – {f_2} {f_2} – {f_2}} \ gauche ({\ commencez {array} {* {20} {* {20} {* {20} {* {20} {* {20} {* {20} {* } 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0
1 & 0 \ fin {array}} \ droite) \)
\ (\ Mathop \ to {f_4 _4} {f_4} – {f_3}} \ gone ({\ commencez {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1
{- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \ fin {array}} \ droite) \)
la matrice Arca Lonada a 3 lignes LI (sa gamme est 3), puis nous pouvons affirmer que la taille de \ (S + T \) est 3.
Comme la dernière ligne a été annulée, le vecteur \ (\ gauche ({{0.0 0,0} \ droite) \) est une combinaison linéaire des trois autres, donc une base de \ (S + T \) est: \ ({b_ {s + t}} = \ gauche {{\ gauche ({1, – 1,0,1} →, \ gauche ({0,1,0, 0} → \ GAUCHE ( {1.0, – 1.1} \ droite)} \ Right \ \ \ \ \ \ \ \).
Rappelez-vous que les rangées de la matrice étagère constituent une autre base de la somme:
\
somme directe
La quantité de deux sous-espaces est directe si et uniquement si l’intersection de la sous-facios est le vecteur zéro.
Lorsque la somme est directe est écrite:
\
Exemples \ ({\ rm {v} = {\ mathbb {r} ^ 3} \)
Ensuite, nous examinerons différentes sommes de somme de somme de sous-espaces dans \ (\ \ mathbb {r} ^ 3} \ ).
deux droites
un cas possible de la somme de deux sous-espacios dans \ ({\ mathbb {r} ^ 3} \) est celle de deux droites qui sont coupées :
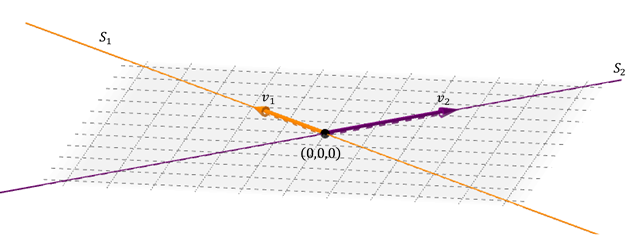
L. OS Deux vecteurs droits Li génèrent une carte: celle qui contient les deux droites. La somme est directe car l’intersection entre les lignes est le vecteur nul.
\
\ ( {S_1} \ opus {s_2} = s \) où \ (S \) est le plan contenant les deux lignes
deux plans coupés
un autre cas possible de la somme de Deux sous-espaces dans \ (\ \ mathbb {r} ^ 3} \) est le deux dessin de deux dessins: 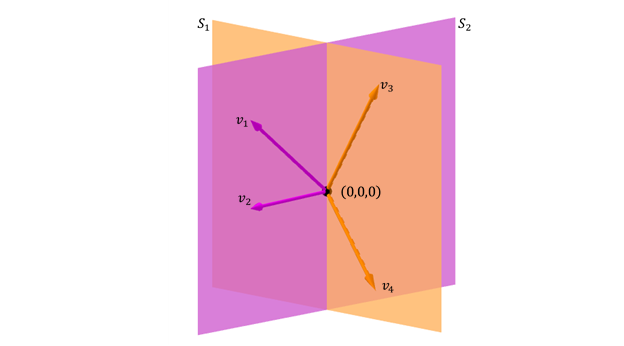
\}} = gène \ gone \ {{{\ \; {v_1}, {v_2}, {v_3}} \ rightht \} \]
la somme du Subspacios est \ ({\ mathbb {r} ^ 3} \), mais ce n’est pas une somme directe car l’intersection n’est pas le vecteur zéro:
\
un plan et une droite inclus dans l’avion
Un autre cas possible de deux sous-espaces dans \ ({\ mathbb {r} ^ 3} \) est celui d’un appartement et un droit inclus dans l’avion. 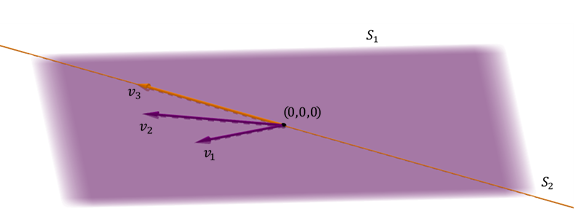
\
Le même plan est obtenu et la somme n’est pas directe Parce que l’intersection n’est pas égale au vecteur zéro.
un plan et une droite non inclus dans le plan
Un autre cas possible de la somme de deux sous-appacios in \ ({\ \ \ mathbb {r} ^ 3} \) est celui d’un plan et d’une ligne droite non incluse dans l’avion. 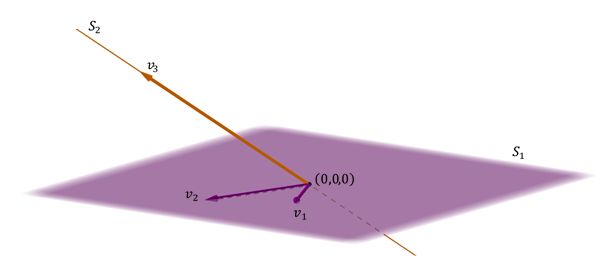
\
est généré \ ({\ mathbb {r} ^ 3} \ ) Parce que le directeur de vecteur de la ligne ne fait pas fonctionner avec les vecteurs d’avion, et il est également direct car l’intersection est NULL vecteur:
\
Observation: dans le dernier cas, L’union des bases des deux sous-espaces forme une base de tout espace. Dans ce cas, chaque vecteur de \ (\ \ mathbb {r} ^ 3} \) peut être exprimé de manière unique en tant que somme d’un vecteur de \ (_1} \) et d’une autre de \ ({s_2} \).
Exercice pour le lecteur 3
DIC \ ({S_1} = Gen \ Gauche \ {{\ {\ {\ {{1,2,1} \ droite), \ \ \ GAUCHE ({ 0.2,0} \ droite)} \ right \ \ \ \ \ \ \ \ ({s_2} = \ gauche {\ gauche ({x, y, z} \ droite): \ \; \; x + y = y – Kz = 0} \ droite \} \),
a) trouver les valeurs de \ (k \) pour lesquelles \ ({s_1} \ opus {s_1} = {\ mathbb {r} ^ 3} \).
b) pour \ (k = 0 \), vérifiez que \ (v = \ gauche ({3,2,2,2 \ \ droite) \) peut s’exprimer dans une manière unique comme une somme d’un vecteur \ ({v_1} \ in {s_1} \) et d’une de \ ({v_2} \ in {s_2} \ \).
Exercice pour le lecteur 4
sont les sous-appacios de \ (\ \ mathbb {r} ^ 4} \):
\ (S = gène \ gauche {\ gauche ({1,1,1, 1} \ droite), \ \ goned ({0,1,0,1} \ droite)} \ right \ \ \ \ \ \ \ \ \ (t = \ gauchée \ {{\ {gauche ({x, y, z, t} → : \; \; \; \; \; \; xz + t = 0} \ droite \} \)
Laquelle des affirmations suivantes est correcte? Justifier.
- \ (s \ opus t = {\ mathbb {r} ^ 4} \)
- \ (s + t = {\ mathbb {r} ^ 4} \)
- \ (s + t = w \; \; \; et \; \ dim \ gauche (w \ droite) = 3 \)
- \ (S \ OPLUS T = w \) et \ (\ dim \ gauche (w \ droite) = 3 \)
théorème de la dimension de la somme
si \ ({ S_1} \) et \ ({s_2} \) sont des sous-espaces d’un espace vectoriel \ (v \) (dimension finie), puis:
\
Dans le cas particulier que la somme est directe, telle que \ ({s_1} → {_2} = \ gauche {{{{{{0_v}} \ droite \} \ ), c’est:
\
Exemple
donné le sous-espacios \ ({p_2} \):
\
\
Trouvez des bases des deux sous-espaces et de l’intersection
Résolution
Nous trouvons une base de \ ({s_1} \):
\
Alors sont les polynômes de la forme:
\
alors une base de \ ({s_1} \) est la suivante:
\
Nous trouvons une base de \ ({s _2} \):
\
Les polynômes de la forme:
\
\
à rechercher \ ({s_1} · \ cap {s_2} \) Nous devons considérer que les équations de \ ({S_1} \) et aussi ceux de \ (_2} \):
\
Les polynômes seront sous la forme:
\
alors:
Notez que comme nous connaissons les dimensions de \ (_1} \), \ ({s_2} \) et \ ({s_1} · {s_2} \), nous pouvons calculer la dimension de \ ({s_1} + {s_2} \):
\
mais le seul sous-espace de \ ({p_2} \) avec dimension 3 est \ ({p_2} \) . Alors: \ ({s_1} + {s_2} = {p_2} \ \).
Exercice pour le lecteur 5
Compte tenu des sous-espacios de \ ({\ mathbb {r} ^ {2 \ fois 2}} \):
\
a) Trouvez des bases de \ ({w_1} \) et \ ({w_2} \)
b) obtenir \ ({w_1} → _2} \).
c) sans trouver \ ({w_1} + {w_2} \) analysez la validité de l’affirmation suivante:
\
d) propose une base de \ (\ mathbb {r} 2} \) formée par des matrices symétriques et anti-immémérétriques et exprime le tableau
\
comme une matrice symétrique plus un antishymétrique.
produit interne
dans la première unité que nous Scaréd produit scalaire entre les vecteurs et leurs applications à la géométrie. Dans cette section, nous proposons de généraliser cette opération à d’autres espaces vectoriels, définissant la notion générale du produit interne des propriétés du produit scalaire.
Définition: un produit interne dans un véritable espace vecteur \ (V \) est une opération qui attribue à chaque couple de vecteur \ (u \) et \ (v \) de \ (v \) un nombre réel \ (u \; v \) tel que les propriétés suivantes sont vérifiées (pour Tout vecteur \ (u, \; v, \; v \) de \ (v \) et de tout scalaire \ (\ alpha \)): 1. \ (U \ CDOT V = V \ CDOT U \)
2. \ (U \ CDOT \ Gauche ({v + w} \ droite) = \ Gauche ({U \ CDOT V} \ ROIGE) + \ loft ({U \ CDOT W} \ ROID) \)
3. \ (α u \ cdot v = \ alpha \ gone ({u \ cdot v} \ droite) \)
4. \ (Uu ≥ \ ge 0 \; \; uu = 0 \; \; \; \ « \ leftrightarrow \ \; \; \; \; \; \; u = {0_v} \ u = {0_v} \ u = \ \
IT est possible de définir différents produits internes dans un espace vectoriel (pendant que ces propriétés sont vérifiées). Dans notre sujet, nous ne travaillerons qu’avec le produit interne canonique dans \ ({\ mathbb {r} ^ n} \), qui est la propagation du produit de l’échelle:
\ (\ gone ({{x_1}, {x_2} \ ldots, {x_n}} \ droite). \ Gauche ({{y_1}, {y_2}, \ ldots, {y_n}} \ droite) = {x_1} {y_1} + {x_2} {y_2} + \ ldots {x_n} {y_n} \) produit interne canon dans \ (\ mathbb {r} ^ n \)
Cette définition nous permet d’étendre le concept d’orthogonalité à \ ({\ mathbb {r} ^ n} \):
\ (u \ bot v \; \ \ \ leftrightarrow \; \; uv = 0 \) Etat d’orthogonalité
Exemple
Effectuons le produit interne de \ ({ \ Mathbb {r} ^ 4} \):
\
as \ (uv = 0 \) puis \ (u \) et \ (v \) sont orthogonaux. \ (\; \ \)
complément orthogonal d’un sous-espace
Soit \ (s \) sous-espace de \ (v \) (espace vectoriel avec produit interne).
Le complément orthogonal de \ (s \), que nous désignons comme \ ({s \ bo T} \), est l’ensemble de vecteurs de \ (v \) qui sont orthogonaux à chacun des vecteurs de \ (s \):
propriété: \ ({s ^ \ bot} \) est un sous-espace de \ (v \).
1. \ ({0_v} \) appartient à \ ({s \ bot} \) comme \ ({0_v} .w \; = \ \; 0 \) pour tout \ (W \) de \ (s \)
2. Sean \ (u, v \ in {s ^ \ bot} → 0 \ wedge vw \; = \ \; 0 \; \; \; \ Fordall w \ in s \ rightarrow \ gauche ({u + v} \ droite) .w \; = \; uw \; + \; v.W \; = \; 0 \)
donc \ (u + v \) est dans \ ({s ^ \ bot} \)
3. Oui \ (u ~ {s ^ \ bot} → {^ ^ \ bot} \). Pourquoi?
Exemple 1
Sea \ (S = \ Gauche \ {\ gauche ({x, y, z} \ droite) \ in {\ mathbb {r} ^ 3 } \; | \; 2x + 3 et – z = 0} \ droite \} \). Trouver \ ({s ^ \ bot} \).
Résolution
Nous devons rechercher \ ({\ mathbb {r} ^ 3} \) perpendiculaire à tous vecteurs de ce plan.
Nous recherchons d’abord une base de \ (s \), par exemple:
Pour trouver le complément orthogonal, nous recherchons tous les vecteurs \ (\ gone ({x, y, z} \ droite) \) qui sont orthogonaux à \ (\ {- 1 ,, 1.1} \ droite) \ ) Ya \ (\ gauche ({0,1,3} \ droite) \).
Système d’équations définissant le complément orthogonal:
\
\
Qu’est-ce qu’une base de sous-espace \ ({s ^ \ bot} \)?
\
La base est un vecteur perpendiculaire à l’avion \ (s \). Par conséquent, le complément orthogonal d’un avion qui passe à travers l’origine est la ligne perpendiculaire qui passe à travers l’origine.
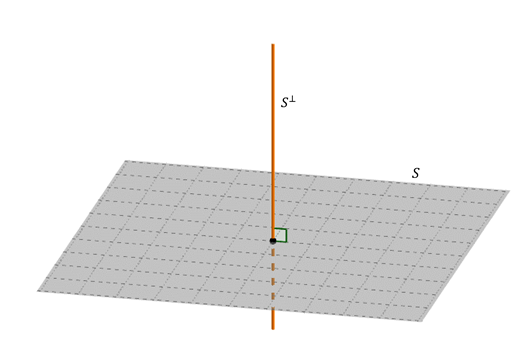
Oui \ (s \) est une ligne qui passe à travers la source: quel est votre complément orthogonal?
Exercice pour le lecteur 6
justifier la procédure que nous utilisons pour trouver les équations de \ (^ \ bot} \), nous nous demandons de démontrer la propriété suivante:
Sean \ (U, \; v, \ ; W \) vecteurs de \ ({\ mathbb {r} ^ n} \).
si \ (w \) est orthogonal à \ (u \) déjà \ (v \), alors est orthogonal à une combinaison linéaire de \ (u \) et \ (v \ (v \).
exemple 2
donné sous sursacace \ ({\ mathbb {r} ^ 4} \ ):
\
base de halle et dimension du complément orthogonal.
Résolution
Nous devons rechercher les vecteurs de \ ({\ mathbb {r} ^ 4} \) qui sont orthogonaux aux vecteurs \ (s \).
Nous trouvons une base de \ (s \ ):
\
\
Nous recherchons \ ( \ Gauche ({{x_1}, {x_2}, {x_3}, {x_4} \ \ droite) \) telle que:
Nous trouvons les équations qui définissent \ (^ \ bot} \):
\
cherche une base de \ (^ \ bot } \):
\
\
Propriétés du complément Ortogonal
Sea \ (v \) Un espace de vecteur de dimension fine, avec produit interne et être \ (s \) un sous-espace de \ (v \). Ensuite, les propriétés suivantes sont vérifiées:
- \ ({\ gauche ({^ \ bot}} \ s \ bot} = s \)
- \ ({v ^ \ bot} = \ gone \ {{{\; {0_v} \;} \ right \} \) et \ (\ \ {\ \; {0 {v \;} }} \ Droite \} {\; \ bot} = v \)
- \ \ ^ ^ \ bot} = \ ^ {{{{{0_v}} \ rightsht \) \)
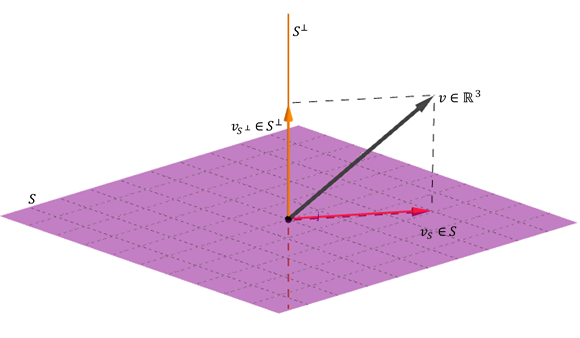
- \ (s + {s ^ \ bot} = v \)
Cette dernière propriété signifie que n’importe quel vecteur \ (v \) peut s’exprimer comme une somme d’une somme d’un Vecteur de plus autre que \ ({s ^ \ bot} \).
illustrer avec un exemple géométrique de \ (\ mathbb {r} ^ 3} \):
de propriétés 3 et 4 est déduit:
et donc:
la liaison d’une base \ (s \) avec une base de \ ({s ^ \ bot} \) est la base de \ (v \). Ceci s’applique à étendre une base de \ (\; \) à une base de \ (v \), comme indiqué comme l’exemple suivant.
Exemple
Sea \ (S = \ gauche \ {{\ \ {{{x_1}, {x_2}, {x_3}, {x_4}} \ droite) \ in {\ mathbb {r} ^ 4} \ ;: \; \; \ \; \; \; \; \; \; {x_4} = 0 \; \; \; \; \; \ x_1} – {x_2} + 3 {x_4} = 0 \;} \ droite \} \).
trouver une base de \ ( S \) et l’étendez à une base de \ (\ mathbb {r} ^ 4} \).
Résolution
Nous recherchons un S, par exemple:
\
comme \ (dim \ gauche (s \ droite) = 2 \), nous pouvons anticiper que: \ (sombre ^ \ Bot} \)) = 4-2 = 2
de la base de S, nous obtenons les équations de \ (^ \ bot} \):
\
et nous trouvons une base de \ (^ \ bot} \), par exemple:
\
Ensuite, rejoignez les bases de \ (s \) et \ ({s ^ \ bot} \) – 2.0, – 1} →), \ Gauche ({0.0,1,0} \ à droite), \ Gauche ({2,1.0.0} \ droite), \ Gauche ({0.1.0, – 2} \ droite )} \ droite \} \) base de \ (\ \ mathbb {r} ^ 4} \)
Exercice pour le lecteur 7
dés Le sous-AppAccios suivant \ ({\ mathbb {r} ^ 4} \):
\ (S = \ Gauche {{\ \ Gauche ({{x_1}, {x_2}, {x_3}, {x_4}} \ droite) \ \; \; \; \; \; \; \; \; \; \; {x_2} + 2 {x_3} = 0 \;} \ right \} \) et \ (w = (w = gène \ gauche {{\ \ \ \ « gauche ({1,0.0.0} \ droite), \ GAUCHE ({ 2,3, k, 0} \ droite)} \ droite \} \)
trouver les valeurs de \ (k \) pour lesquelles \ (w = \; {s ^ \ bot} \).