intersezione
sean \ (s \) e \ (t \) subrespacios dello stesso spazio vettoriale \ ( V \). Definiamo l’intersezione come segue:
\ (\ Cap T = \ Sx {{v \ in v \ ;; ; \; \ Wedge \; \; v \ in t} \ giusto \ \ \ in t} \ destra \} \; \) intersezione del sottospazio
proprietà
\ (s \ cap t \) è subspace di \ (v \)
Dimostrazione
1. \ ({0_V} \ in s \ wedge {0_v} \ in t \ reapyarrow {0_v} \ in s \ cap t \)
2. Considera \ (u, \; v \; \ in \; · \)
\
\\]
\\]
di e è dedotto questo \ (u + \; v \; \ \ \; \)
3. Lasciamo il lettore dal lettore per dimostrare:
\
Esempio 1
visto il subspacios de \ ({\ mathbbs {r} ^ 3} \ ):
\
\
Trova \ (S \ Cap T \).
Risoluzione
per definizione \ (s \ cap t \) è un set che sarà formato dai vettori che appartengono a \ (s \) e \ (t \). Cioè, quei vettori che soddisfano le equazioni di \ (s \) e quelle di \ (t \):
\
è circa Un dritto definito come intersezione di due piani. Una base del dritto è un vettore direttore.
geometricamente possiamo cercare il direttore vettoriale come prodotto vettoriale dei vettori normali degli aerei:
\
\
quindi \ (\ sinistra \ \; \ \ sinistra ({3, – 2,1} destra) \;} \ Destra \}} \) è una base di \ (s \ cap t \).
Un altro modo per risolverlo è quello di cercare la soluzione Soluzione di sistema:
\
\
E poi arriviamo a questo \ (\ Sinistra \ \; {3, – 2.1} \ Destra) \;} \ destra \} \ \) è una base di \ (s \ cap t \).
Esempio 2
Be the sub -sites di \ ({\ mathbb {r} ^ {2 × 2}} \):
\
\
trova \ (s \ cap t \).
Risoluzione
Risoluzione
L’intersezione del sottospazio è formato dai vettori che verificano le equazioni di detti sottospazi.
Cosa deve essere soddisfatta una matrice per appartenere a \ (s \)?
\
Che cosa deve essere soddisfatta una matrice per appartenere a \ (t \)?
deve essere in grado di essere scritto come una combinazione lineare di: \ (\ sinistra ({\ \ begin {array} {*} {20} {c}} 1 & 0 \\ 2 & {- 1} \ end {array}} \ destra) \; e \ sinistra ({{{20} {c}} 1 & 0 \\ 1 & 0 \ end {array}} \ destra) \)
Troviamo le equazioni del sottospazio \ (t \):
\
\
\
\
Consideriamo ora che le matrici di \ (S \ Cap T \; \) devono rispettare le equazioni di \ (s \) e quelle di \ (T \):
\
che è:
\
> Allora le matrici di \ (s \ cap t \) sono il modulo:
\
e una base di \ (s \ bed T \) it:
\
C’è un metodo alternativo più breve per trovare una base di \ (s \ c AP T \) senza la necessità di ottenere le equazioni di \ (t \), poiché vedremo sotto.
Scriviamo una matrice di \ (T \) come una combinazione lineare dei vettori che generano IT:
Ma in aggiunta, le equazioni di \ (s \) che stabiliscono che \ (c = b \) dovrebbero essere soddisfatte. Quindi:
\
Pertanto, una matrice di \ (s \ cap t \) è:
\
SUMIO dei sottospettitori
Dato \ (s, \; t \; \) subrespacios de \ (v \), la somma come segue:
\ (s + t = \ sinistra \ {{v \ in v \ ;: \; \; w = {v_1} + {v_2} \; \;, \; \; with \; \; {v_1} \; {v_1} \; {v_1} \; {v_2} \; {v_2} \; {v_2} \; {v_2} \ in t} \ Rightht \) somma di subspacios
Proprietà: \ (S + T \) è una subspace dello spazio vettoriale \ (v \).
Lasciamo la dimostrazione dal lettore.
Se conosciamo set s e T Generatori, possiamo trovare generatori di somma:
\ (s = genice \ sinistra {{{{{{{v_1}, {v_2}, \ Ldots, {v_q}} \ destra \} \) e \ (t = gene \ sinistra {{{{w__1}, {w_2}, \ ldots, {w_r}} \ destra \} \) \ (\; \ dama dama \; S + t = gen \ sinistra {{{v_1}, {v_2}, \ ldots {v_q}, {w_1}, {w_2}, \ ldots, {w_r}} \ destra \} \)
Per trovare la somma è normale per cercare le basi di \ (S \) e \ (T \). Poiché le basi sono gru generatori di Li, se conosciamo una base di ogni subspazio possiamo ottenere un set di generatore set:
date le basi:
\ ({B_S} = \ SINISTRA \ {{{V_1}, {V_2,}, {V_2, \ LDOTS, {V_Q}}} Destra \} \) e \ ({B_T} = \ Sinistra {{{W_1}, {W_2}, \ ldots, {w_r}} \ destra \} \)
Risultati:
\ (\ sinistra \ {{\ V_1}, \ ldots, {v_q}, {w_1}, \ ldots, {w_r}} \ destra \}}) set generatore di somma.
Osservazione: un set di generatore della somma è quindi ottenuto ma non è sempre indipendente linearmente indipendente.
- Se sei Li, troviamo una base di La somma.
- Se è LD, possiamo estrarre una base dalla somma eliminando i vettori “sobran”.
Esempio 1
Dato i seguenti sottospace \ (v = {\ mathbb {r} ^ 3} \):
\
\
Siamo interessati a trovare \ (s + t \).
Cerchiamo una base di \ (s \). Per quello nell’equazione cancellando una variabile:
\
Ora impostiamo un vettore generico:
\
\
Trova una base di \ (t \). Per questo nell’equazione cancella una variabile:
\
Ora impostiamo un vettore generico:
\
Allora
\
\
Sappiamo che tutti i set di più di 3 vettori in \ ({\ mathbb {r} ^ 3} \) dipendono linearmente, poiché la dimensione di \ ({\ mathbb {r} ^ 3 } \) It 3. Come possiamo estrarre una base dalla somma?
Potremmo mettere insieme una matrice con questi 4 vettori e portarlo alla forma a gradini. O se no, come lo spazio è \ ({\ mathbb {r} ^ 3} \) possiamo pensare geometricamente:
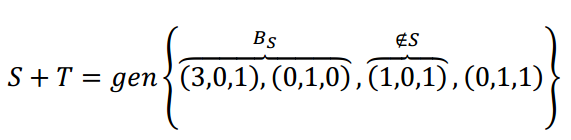
Come \ (\ sinistra ({1,01,1} \ destra) \) non verifica l’equazione del piano S, i primi 3 vettori non sono coplani e quindi formano una base di \ (\ mathbb {r} ^ 3 \) . Possiamo eliminare \ (\ sinistra ({0,1,1} \ destra) \) perché è una combinazione lineare di detta base.
Pertanto: \ (B = \ Sinistra {{\ Sx ({3.0 .1} \ destra), \ sinistra ({0,1.0} \ destra), \ sinistra ({1,01} \ destra)} \ destra \} \) è base di \ (s + t \) ed è base di \ (\ MathBB {R} ^ 3 \).
In questo caso, come \ (S + T \; \) è un sottospazio di \ ({r ^ 3} \) dimensione 3 , possiamo affermare che:
\
Generalizzazione:
\ (S \) subspace \ (v \) e \ (\ dim \ sinistra (s \ destra) = \ dim \ sinistra (v \ destra) \ raddopping s = v \)
Esempio 2
Dato i seguenti sottogruppi di \ (v = {\ mathbb {r} ^ 4} \):
\
\
Trova base e dimensione di \ ({s_1} + {s_2} \; \).
Risoluzione
\
\
\
\
\
Come abbiamo visto, a Metodo per analizzare se s Su Li o LD, consiste nell’assemblare una matrice con i vettori come le file e portarlo alla sua forma a gradini. Per comodità posizioneremo i vettori nel seguente ordine:
\ (\ sinistra ({\ begin {array} {20} {c}} 1 & {- 1} & 0 & 1 \\ 1 & 0 & {- 1} & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 1 & 0 \ end {array}} \ destra) \)
\ (\ Mathop \ a {f_2} {f_1}} \ sinistra ({\ begin {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array} } \ destra) \) /p>
\ (\ mathop \ to} – {f_2} {f_3}} {f_2}} \ \ sinistra ({\ begin {array} {* {20} {c} } 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \ End {array}} \ destra) \)
\ (\ MathOP \ a {f_4 _4} {f_4} – {f_4}} {f_3}} \ \ sinistra ({\ begin {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \ end {array}} \ destra) \)
the arca matrice Lanada ha 3 righe LI (la sua gamma è 3), quindi possiamo affermare che la dimensione di \ (S + T \) è 3.
Come l’ultima riga è stata annullata, il vettore \ (\ sinistra ({{0,0,0} \ destra) \) è una combinazione lineare degli altri tre, quindi una base di \ (S + T \) è: \ ({b_ {s + t}} = \ sinistra {{\ sinistra ({1, – 1,01} →, \ sinistra ({0,1,0, 0} → \ sinistra ( {1.0, – 1.1} \ destra)} \ destra \}} \ \).
Richiamare che le righe della matrice a gradini costituiscono un’altra base della somma:
\
Sum Direct Sum
La quantità di due sottospazi è diretta se e solo se l’intersezione dei subacios è il vettore zero.
Quando la somma è diretta è scritta:
\
Esempi in \ ({\ rm {v} = {\ mathbb {r} ^ 3} {r} ^ 3} \)
Avanti considereremo diverse somme di somma di sottospace in \ ({\ mathbb {r} ^ 3} \ ).
Due rettilinei
Un possibile caso di somma di due sottospacios in \ ({\ x mathbb {r} ^ 3} \) è quello di due rettilinei dritti che vengono tagliati :
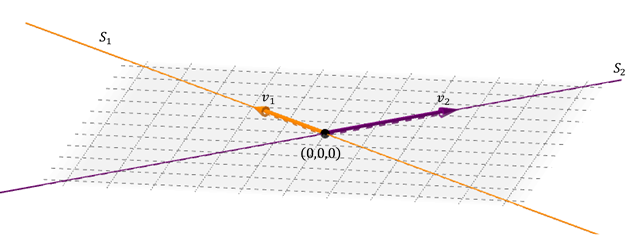
l. OS Due vettori diritti Li Genera una mappa: ciò che contiene sia i lineari. La somma è diretta perché l’intersezione tra le linee è il vettore nullo.
\
\ ( {S_1} \ opus {s_2} = s \) dove \ (s \) è il piano contenente le due linee
due piani tagliati
un altro caso possibile di somma di Due sottospace in \ ({\ MathBB {R} ^ 3} \) è il tasto disegno di due disegni:
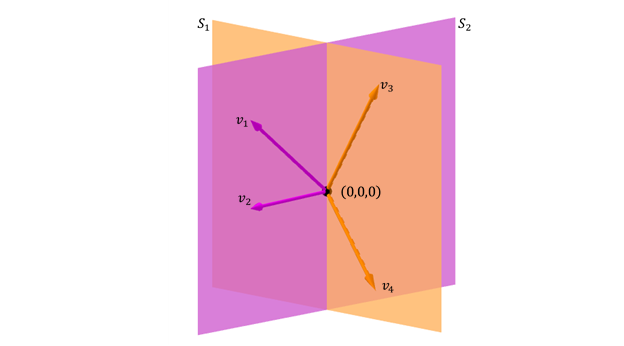
\}} = Gene \ sinistra \ {{\; {v_1}, {v_2}, {v_3}} {v_3}} \ Rightht \} \]
La somma del subspacios è \ ({\ mathbb {r}}} \) ma non è una somma diretta perché l’intersezione non è il vettore zero:
\
A Piano e un piano incluso nell’aereo
Un altro caso possibile di due sottospazie in \ ({\ mathbb {r} ^ 3} \) è quello di un piatto e dritto incluso in l’aereo. 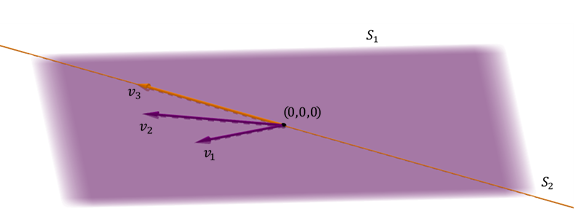
\
Lo stesso piano è ottenuto e la somma non è diretta Perché l’intersezione non è uguale al vettore zero.
Un piano e un diritto non incluso nel piano
Un altro caso possibile di somma di due sub-appassioni in \ ({\ mathbb {r} ^ 3} \) è quello di un piano e di un diritto non incluso nel piano. 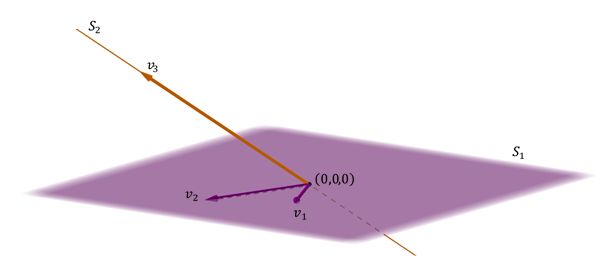
\
è generato \ ({\ MathBB {R} ^ 3} \ ) Poiché il direttore vettoriale della linea non ha affrontato i vettori aerei, ed è anche diretto perché l’intersezione è null vettoriale:
\
osservazione: nell’ultimo caso, L’unione delle basi dei due sottospazi costituisce una base di tutto lo spazio. In questo caso, ogni vettore di \ ({\ mathbb {r} ^ 3} \) può essere espresso in modo unico come somma di un vettore di \ (_1} \) e un altro di \ ({s_2} \).
Esercizio per lettore 3
Dice \ ({s_1} = gen \ sinistra \ {{\ \ sinistra ({1,2,1} destra), \ \ \ sinistra ({ 0,2,0} \ destra)} \ destra \} \) e \ ({s_2} = \ sinistra {\ sinistra ({x, y, z} \ destra): \; \; \; x + y = y – KZ = 0} \ destra \} \),
a) Trova i valori di \ (k \) per quale \ ({s_1} \ opus {s_1} = {\ mathbbs {r} ^ 3} \).
b) per \ (k = 0 \), verificare che \ (v = \ sinistra ({3,2,2,2 \ destra) \) possa esprimersi in un modo unico come una somma di un vettore \ ({v_1} \ in {s_1}} \ in \ \ ({v_2} \ in {s_2} \).
Esercizio per lettore 4
sono i sub-appacos di \ ({\ mathbb {r} ^ 4} \):
\ (s = genice \ sinistra {\ \ \ sinistra ({1,1,1, 1} \ destra), \ \ \ sinistra ({{0,1,01} \ destra)} \ destra \} \) e \ (t = \ sinistra \ {{\ \ sinistra ({x, y, z, t} → : \; \; \;, \; \; xz + t = 0} \ giusto \} \)
Quale delle seguenti affermazioni è corretta? Giustificare.
- \ (s \ opus t = {\ \ mathbb {r} ^ 4} \)
- \ (s + t = {\ mathbbs {r} ^ 4} \)
- \ (s + t = w \; \; \; e \; \ win \; e \; \ dim \ sinistra (w \ destra) = 3 \)
- \ (s \ oplus T = w \) e \ (\ dim \ sinistra (w \ destra) = 3 \)
teorema della dimensione della somma
si \ ({ S_1} \) e \ ({s_2} \) sono sub-spazi di uno spazio vettoriale \ (v \) (dimensione finita), quindi:
\
nel caso particolare che la somma è diretta, ad esempio \ ({s_1} → {_2} = \ sinistra {{{{{{0_V}}} destra \} \ ), è:
\
Esempio
Dato il subspacios \ ({p_2} \):
\
\
Trova basi di entrambi i sottospazi e l’intersezione
Risoluzione
Troviamo una base di \ ({s_1}} \):
\
Allora sono i polinomi del modulo:
\
Quindi una base di \ ({s_1} \) è:
\
Troviamo una base di \ ({s _2} \):
\
Allora i polinomi del modulo:
\
\
per cercare \ ({s_1} \ \ cap {s_2} \) Dobbiamo considerare che le equazioni di \ ({S_1} \) e anche quelli di \ (_2} \):
\
I polinomi saranno nel modulo:
\
Allora:
\
Si noti che come conosciamo le dimensioni di \ (_1} \), \ ({s_2} \) e \ ({s_1} · {s_2}}), possiamo calcolare la dimensione di \ ({s_1} + {s_2} \):
\
Ma l’unico subspazio di \ ({p_2} \) con dimensione 3 è \ ({p_2} \) . Quindi: \ ({s_1} + {s_2} = {p_2}}).
Esercizio per il lettore 5
Dato il sottospacios de \ ({\ mathbb {r} ^ {2 \ volte 2}} \):
\
\
> a) Trova basi di \ ({w_1} \) e \ ({w_2} \)
b) Get \ ({w_1} → _2} \).
c) senza trovare \ ({w_1} + {w_2}}} analizzare la validità della seguente affermazione:
\
D) propone una base di \ ({\ mathbb {r} 2} \) formato da matrici simmetriche e anti-immersione e esprimono l’array
\
come matrice simmetrica più un antisishymetrico.
Prodotto interno
Nella prima unità noi Sega il prodotto scalare tra i vettori e le loro applicazioni alla geometria. In questa sezione proponiamo di generalizzare questa operazione ad altri spazi vettoriali, definendo la nozione generale del prodotto interno dalle proprietà del prodotto scalare.
Definizione: un prodotto interno in un vero spazio vettoriale \ (V \) è un’operazione che assegna a ciascuna coppia vettoriale \ (u \) e \ (v \) di \ (v \) un numero reale \ (u \; v \) come le seguenti proprietà vengono verificate (per Tutti i vector \ (u, \; v, \; w \) di \ (v \) e tutto scalano \ (\ alfa \)): 1. \ (U \ cdot v = v \ cdot u \)
2. \ (u \ cdot \ sinistra ({v + w} \ destra) = \ sinistra ({u \ cdot v} \ destra) + \ loft ({u \ cdot w} \ destra) \)
3. \ (α u \ cdot v = \ alfa \ sinistra ({u \ cdot v} \ destra) \)
4. \ (Uu ≥ \ Ge 0 \; \; uu = 0 \; \; \; \ leftrightrow \; \; \; \; u = {0_v} \) /p>
it è possibile definire diversi prodotti interni in qualsiasi spazio vettoriale (mentre queste proprietà sono verificate). Nel nostro soggetto, funzioneremo solo con il prodotto interno canonico in \ ({\ MathBB {R} ^ N}}, che è la diffusione del prodotto in scala:
Questa definizione ci consente di estendere il concetto di ortogonalità a \ ({\ mathbb {r} ^ n} \):
\ (u \ bot v \; \; \ \ leftrightarrow \; \; uv = 0 \) condizione di orthogonalità
Esempio
Eseguiamo il prodotto interno di \ ({ \ MathBB {R} ^ 4} \):
\
\
come \ (UV = 0 \) Allora \ (u \) e \ (v \) sono ortogonali. \ (\; \)
Complemento ortogonale di un sottospazio
Let \ (s \) subspace di \ (v \) (spazio vettoriale con prodotto interno).
il complemento ortogonale di \ (s \), che indicano come \ ({s \ bo T} \), è il set vettoriale di \ (v \) che è ortogonale a ciascuno dei vettori di \ (s \):
Proprietà: \ ({s ^ \ bot} \) è un sottospazio di \ (v \).
1. \ ({0_V} \) appartiene a \ ({S \ Bot} \) come \ ({0_V} .w \; = \; 0 \) per tutto \ (w \) di \ (s \)
2. Sean \ (u, v \ in {s ^ \ bot} → 0 \ wedge vw \; = \; 0 \; \; \; \ fortall w \ in s \ ray raro \ sinistra ({u + v} \ destra) .w \; = \; uw \; + \; v.W \; = \; 0 \)
Pertanto \ (u + v \) è in \ ({s ^ \ bot} \)
3. Sì \ (u ~ {s ^ \ bot} → {^ ^ \ bot} \). Perché?
Esempio 1
mare \ (s = \ sinistra \ {\ sinistra ({x, y, z} \ destra) \ in {\ mathbb {r} ^ 3 } \; | \; 2x + 3 e – z = 0} \ destra \} \). Trova \ ({s ^ \ bot}} \).
Risoluzione
Dobbiamo cercare \ ({\ mathbb {r} ^ 3} \) che sono perpendicolari a tutti Vettori di quell’aereo.
Prima cerchiamo una base di \ (s \), ad esempio:
\
Per trovare il complemento ortogonale, cerchiamo tutti i vettori \ (\ sinistra ({x, y, z} \ destra) \) che sono ortogonali a \ (\ sinistra ({- 1 ,, 1.1} \ destra) \ ) Ya \ (\ sinistra ({{0,1,3} \ destra) \).
Un sistema di equazioni che definiscono il supplemento ortogonale:
\
\
Che cos’è una base subspace \ ({s ^ \ bot} \)?
\
La base è un vettore perpendicolare al piano \ (s \). Pertanto, il complemento ortogonale di un piano che passa attraverso l’origine è la linea perpendicolare che passa attraverso l’origine.
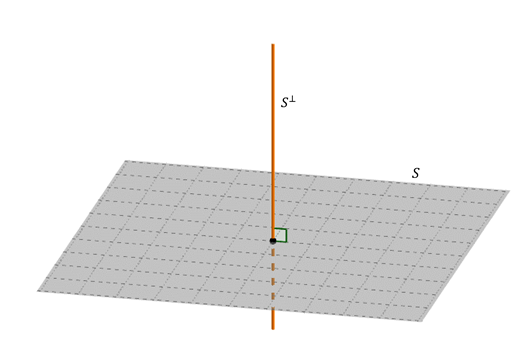
sì \ (s \) è una linea che passa attraverso la fonte: qual è il tuo supplemento ortogonale?
Esercizio per lettore 6
Per giustificare la procedura che utilizziamo per trovare le equazioni di \ (^ \ Bot} \), chiediamo di dimostrare la seguente proprietà:
sean \ (u, \; v, \ ; W \) vettori di \ ({\ mathbb {r} ^ n} {r} ^ n} \).
si \ (w \) è ortogonale a \ (u \) già \ (v \), allora esso è ortogonale a qualsiasi combinazione lineare di \ (u \) e \ (v \).
Esegna 2
Dato il prossimo subspace \ ({\ MathBB {R} ^ 4} \ ):
\
Halle Base e dimensione del complemento ortogonale.
Risoluzione
Dobbiamo cercare i vettori di \ ({\ MathBB {R} ^ 4} \) che sono ortogonali ai vettori \ (s \).
Troviamo una base di \ (s \ ):
\
\
Ora stiamo cercando \ ( \ SINISTRA ({{X_1}, {X_2}, {X_3}, {X_4}}} Destra) \) Tale che:
\
Troviamo le equazioni che definiscono \ (^ \ Bot} \):
\
Cerca una base di \ (^ \ Bot } \):
\
\
Proprietà del complemento Orgogonal
mare \ (v \) A Spazio vettoriale dimensione fine, con prodotto interno e essere \ (s \) un sottospazio di \ (v \). Quindi vengono verificate le seguenti proprietà:
- \ ({\ Sx ({^ \ Bot}} \ Destra) ^ \ Bot} = S \)
- \ ({v ^ \ bot} = \ sinistra \ {{\; {0_v} \;} {0_v} \;} \ destra \} \) e \ (\ sinistra {{\; {0 {v \;} }} \ Destra \} {\; \ bot} = v \)
- \ (s ^ ^ ^ \ \ bot} = \ sinistra \ {{{0_v}} {{0_v}} \ rightsht \) \)
- \ (s + {s ^ \ \ bot} = v \)
Quest’ultima proprietà significa che qualsiasi vettore \ (v \) può esprimersi come una somma di a vettore di altro diverso da \ ({s ^ \ bot} \).
illustrarsi con un esempio geometrico di \ ({\ mathbbb {r} ^ 3} \):
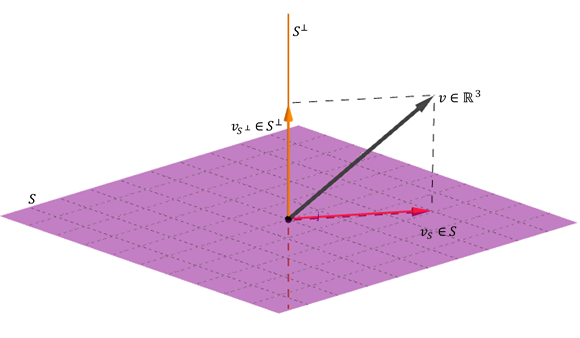
di proprietà 3 e 4 viene detratto:
e quindi:
Il legame di una base \ (s \) con una base di \ ({s ^ bot} \) è base di \ (v \). Questo vale per estendere una base di \ (\; \) a una base di \ (v \), come mostrato come il seguente esempio.
Esempio
mare \ (s = \ sinistra \ {{\ \ sinistra ({{x_1}, {x_2}, {x_3}, {x_4}} \ Destra) \ in {\ mathbb {r} ^ 4} \ ;: \; \; {x_1} +; {x_4} = 0 \; \; \; \; {x_1} – {x_2} + 3 {x_4} = 0 \;} \ destra \} \).
Trova una base di \ ( S \) ed estenderlo a una base di \ ({\ mathbb {r} ^ 4} \).
Risoluzione
Stiamo cercando un s, ad esempio:
\
come \ (dim \ sinistra (s \ destra) = 2 \), possiamo anticipare che: \ (dim ({s ^ \ Bot} \)) = 4-2 = 2
Dalla base delle S, otteniamo le equazioni di \ (^ \ Bot} \):
\
e troviamo una base di \ (^ \ bot} \), ad esempio:
\
Quindi unire le basi dei risultati dei risultati di \ (s \) e \ ({s ^ \ bot} \):
\ (B = \ Sinistra {{\ \ Sx ({1, – 2.0, – 1} →), \ sinistra ({{0,0,1,0} \ destra), \ sinistra ({2,1.0.0} \ destra), \ sinistra ({0.1.0, – 2} \ destra )} \ destra \} \) base di \ ({\ mathbb {r} ^ 4} \)
Esercizio per lettore 7
Dice La seguente sub-Appacios \ ({\ 4}} \ 4} \):
\ (S = \ sinistra {{\ sinistra ({{x_1}, {x_2}, {x_3}, {x_4}} \ Destra) \ ;: \; \; {x_1} = 0 \; \; \; \; {x_2} + 2 {x_3} = 0 \;} \ Destra \} \) e \ (w = genice \ sinistra {{\ \; \ \ sinistra ({1,0.0} \ destra), \ sinistra ({ 2,3, k, 0} \ destra)} \ destra \} \)
Trova i valori di \ (k \) per quale \ (w = \; {s ^ \ bot} \).