Odds in un test del tipo di test

stai facendo a Test del tipo di test, ci sono quattro domande che non sai come rispondere e rispondere erroneamente, ci soturno punti. Se decidi di rispondere alle quattro domande a caso, è più probabile che finisca più punti che se non rispondi a nessuno. Questa affermazione sembra corretta, tenendo conto del fatto che se ci sono quattro domande con quattro opzioni di risposta, è logico presumere che sia più probabile che sia in grado di fallire tre volte e di colpire uno, se assumiamo che tu stia colpisca un punto e fallire Nel caso più probabilmente siamo noi saremo gli stessi. Vale la pena una rosa? La stessa cosa accade con un numero diverso di risposte casuali? Si scopre che la matematica ha qualcosa da dire su di esso …

Esami del tipo di test presenta una serie di risposte da cui devi scegliere, normalmente, una risposta corretta. In alcuni test del tipo di test c’è più di una risposta corretta, a volte i difetti sottraggono i punti, potrebbero esserci risposte ponderate o un limite di domande che possono essere falliti.

Posso approvare se faccio un test di tipo di test senza studio?

L’idea di questo articolo è di rispondere alle domande di stile: posso Approva se faccio un test di tipo di test senza studiare? È la probabilità dalla mia parte se ho risposto a caso? La stessa cosa accade in qualsiasi tipo di test? Qual è la differenza se i difetti sottraggono o se no? Che probabilità devo approvare se rispondo a metà casuale? E se sono sicuro della metà? E per prendere un notevole? E un eccezionale? …

Abbiamo iniziato nel più semplice esame del tipo di test, i successi aggiungono, i guasti e le risposte senza risposta non influiscono sulla nota.

Calcolo della nota. ..

Definiamo alcuni nomi variabili:

n = numero totale di domande
A = Numero di successi
n = Nota finale

Se assumiamo che la nota sia un numero da 0 a 10 e l’esame ha 10 domande il calcolo della nota è banale . La nota ottenuta è uguale al numero di domande di successo:

… con un Baremo

Se l’esame ha una serie di domande diverse dalla Barte della nota, per ottenere la nota finale è necessario dividere il numero di successi tra il numero di domande e moltiplicare dal limite superiore del bordo.

per Esempio: se il Baremo è da 0 a 10 e ci sono 40 domande sull’esame, per estrarre un 5 devi colpire 20 domande. Cioè, numero di domande riuscite tra il numero totale: 20/40 = 0.5 e moltiplicare il risultato del limite superiore del Baremo: 0,5 × 10 = 5.

Generalizzazione, per calcolare una nota in un tipo Test dell’esame in cui i guasti non vengono sottratti e abbiamo un barte:

bₛ = limite del foro superiore

Calcolo delle probabilità …

è abbastanza ovvio che indipendentemente Se sai o non le risposte, se i fallimenti non sottraggono punti, l’opzione migliore è rispondere a tutto. Diciamo che in una questione di punti, non hai, letteralmente, niente da perdere.

In ogni caso, formulamoci la questione con una matematica, quante combinazioni di risposte sono possibili? E come dipende da questo numero?

… con una domanda

Il caso banale è con una singola domanda. Se abbiamo 4 opzioni di risposta: A, B, C, D. Esistono 4 possibilità:

La probabilità che si verifichi un evento è il numero di eventi possibili Tra i tempi l’evento si verifica in questione. In questo caso ci sono 4 eventi possibili, solo 1 comporta la colpire e 3 fallimenti:

la probabilità di colpire la risposta a caso una domanda è da uno tra quattro: 1/4 = 0,25. Normalmente diciamo una probabilità del 25% di colpire.

La probabilità di guasto sarebbe tre tra i quattro: 3/4 = 0,75. Cioè, è del 75%.

Come vediamo, in questo caso una risposta casuale ha tutto da perdere. È anche interessante notare che se aggiungiamo le due probabilità che otteniamo il 100% poiché, in questo caso, ci sono solo due possibili risultati: per colpire o fallire. Vedremo che questo non è il caso se c’è più di una domanda.

In sintesi …

… con due domande (o più)

Con due domande possiamo rispondere ad esempio: A nel primo già nel secondo, A nel primo e B nel secondo, B nel Prima già nel secondo … queste sono tutte combinazioni possibili:

Questi sono, in breve , tutti gli eventi possibili che rispondono a due domande. Sono 16. quattro volte più possibilità che con una domanda. Questo 4 deriva dal fatto che abbiamo 4 opzioni di risposta e cosa succede è che ogni volta che aggiungiamo una domanda che stiamo moltiplicando per 4 le possibili combinazioni di risposte:

P₁ = Numero di opzioni di domanda 1
P₂ = Numero di opzioni di domanda 2
c₂ = Numero di combinazioni di due risposte

La formula sarebbe:

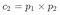
In questo caso:

In generale, devi solo moltiplicare per il numero di opzioni, tutte le volte delle domande ci sono :

Questa formula è facile da semplificare, considerando che il numero di opzioni è sempre lo stesso: p₁ = p₂ = p₃ = … = Pₙ. Se definiamo:

n = numero di domande
p = numero di opzioni in ogni domanda

Il numero di combinazioni è calcolato come segue:

In questo caso, con p = 4 e n = 2:

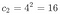
Il prossimo passo è per calcolare le probabilità. In questo caso ci sono tre possibili eventi:

1. successo tutte le domande.
2. Raggiungere una domanda (e fallisce l’altra).
3. fallisci tutto Domande.

Tenendo conto di tutti gli eventi possibili, c’è solo un caso in cui tutte le domande sono accettate, supponendo che le due risposte corrette siano l’ID:

Pertanto la probabilità di colpire le due domande è 1/16 = 6,25%.

Generalizzazione , la probabilità di ottenere tutte le domande di numeri n è 1 tra tutte le possibili combinazioni di risposte, cioè:

Una probabilità del 4,25% è già abbastanza bassa, ma vediamo come questa percentuale diminuisce drasticamente secondo Aumentiamo il numero di domande che rispondiamo a caso. Ad esempio, con 10 domande:

Come vediamo, ci sono più di un milione Possibili combinazioni, quindi, la probabilità di colpire tutte le risposte casuali è minuscola.

… In effetti, è molto più probabile che toccare la lotteria.

Ma non siamo così ambiziosi, non è necessario colpire tutto. Che probabilità è lì per ottenere un po ‘? Supponendo di nuovo che le risposte giuste sono le A, queste sono i tempi che abbiamo ottenuto una risposta a due domande:

>

Nota che non abbiamo evidenziato AA perché sono due successi, non uno.

Abbiamo 6 possibili combinazioni che ci danno una risposta di successo, la probabilità è da sopra la nostra parte:

La probabilità di sollevare qualcosa sarebbe la somma dei due precedenti, o quale è lo stesso, aggiungi La possibilità di ottenere tutto alle possibilità di colpire uno:

non è male, per aver risposto tutto a caso.

L’unica cosa che rimane è conoscere la probabilità di fallire tutto, e dal momento che è l’unico o evento che la nostra probabilità rimane sarà ciò che è pronto per raggiungere il 100%, o quale è lo stesso, il resto delle possibili combinazioni se sottraiamo i successi:

Quindi la probabilità di fallimento supera il cinquanta percento, quindi possiamo scommettere che sicuramente non aggiungeremo punti rispondendo a due domande casuali.

E Quindi la tabella sommaria avrebbe aggiunto le probabilità con due domande: