La visione è il senso con cui otteniamo le maggiori informazioni sul nostro ambiente . L’interpretazione del nostro cervello, sulla base delle informazioni che riceve dagli occhi, è fortemente influenzata dall’esperienza; Questo a volte porta a effettuare errori di apprezzamento. Durante tutto il tempo della tua vita, e soprattutto alle prime età, un individuo categorizzato, generalizza e caratterizza gli elementi dei tuoi dintorni per prendere decisioni rapidamente. Le persone che hanno carenze nel loro senso della vista possono correggere o ridurre i difetti di questo per mezzo di obiettivi, questo è possibile se parliamo di problemi di approccio per esempio. Con lo sviluppo dell’acquisizione di immagini attraverso strumenti tecnologici, è emersa anche la necessità di correggere queste immagini in modo che la sua successiva interpretazione sia vera. Se un dispositivo di acquisizione di immagini fornisce immagini con difetti di messa a fuoco, questa carenza può essere corretta aggiungendo obiettivi al dispositivo. La prospettiva è un aspetto importante durante l’interpretazione di un’immagine, il fondamento di questo aspetto è nell’esperienza, poiché questo è il modo in cui impariamo a stimare misure, posizioni, velocità, ecc. Un’interpretazione accurata dell’immagine ottenuta può essere raggiunta se le caratteristiche dell’oggetto contenute sono note dall’individuo che lo analizza. C’è l’importanza delle proporzioni dell’immagine, per quanto riguarda la realtà, sono congruenti. Usiamo anche la prospettiva per suggerire un’idea a un individuo o persuaderlo, e lì troviamo coraggio quando si tratta di modificare le proporzioni degli elementi in un’immagine. Quando l’immagine acquisita non corrisponde a ciò che vogliamo visualizzare possiamo fare una modifica dell’immagine in modo che sia più conveniente.
Per modificare un’immagine, coordinare le trasformazioni dei pixel e delle modifiche nella luminosità dell’immagine, quest’ultimo è ottenuto con tecniche di interpolazione della luminosità. La modifica delle proporzioni dell’immagine può essere compresa con un’azione analoga: se abbiamo una superficie del ghiaccio ed espandiamo questa superficie con il calore, otterremo una superficie del vapore e ci saranno regioni vuote su detta superficie. Lo stesso effetto avviene nelle immagini e per compensare questo difetto, vengono utilizzate tecniche di interpolazione; Con queste tecniche assumiamo valori a posti vuoti in modo che l’immagine sia apprezzata uniforme, questo è correlato alla risoluzione dell’immagine. Il modo in cui influenzare la geometria dell’immagine si basa sulle tecniche di trasformazione geometrica. Se vogliamo spostare l’immagine, modificare le proprie proporzioni di base e altezza, ruotarlo o scivolare, possiamo eseguire la relativa trasformazione lineare. Se si desidera modificare la geometria dell’immagine senza preservare il parallelismo tra le linee opposte del contorno dell’immagine, possiamo usare una trasformazione bilineale o una trasformazione prospettica. Questa trasformazione utilizza 4 punti di riferimento e 4 punti di trasformazione per definire la funzione di trasformazione.

L’obiettivo di questa pratica è modificare un’immagine di altezza “e” e base “x”. L’immagine verrà modificata da due punti dell’immagine. Per formulare il problema e descrivere la soluzione proposta, verrà utilizzata un’immagine di esempio. Si desidera modificare l’immagine 2, per questo il pixel contrassegnato con un rosso “X” è selezionato e la posizione che è desiderata prendere con un “o” Roj A, per questo caso. Il punto di riferimento “X” avrà le coordinate (PRX (1), PRI (1)). Il punto di riferimento “o” avrà le coordinate (PRX (2), PRIS (2)). Il primo elemento della precedente nomenclatura corrisponde alla posizione sull’asse orizzontale e il secondo elemento corrisponde alla posizione sull’asse verticale. Va tenuto conto del fatto che per individuare questi punti il punto del punto di riferimento è nell’angolo in alto a sinistra dell’immagine.
La trasformazione lineare verrà utilizzata per modificare un’immagine in base alla selezione di due pixel di l’immagine. Innanzitutto, il pixel “1” è selezionato e successivamente il pixel “2”.L’immagine cambierà rispetto a questi due punti di riferimento; Vuoi spostare il pixel “1” alla posizione del pixel “2”, l’intera immagine deve cambiare per adattarsi a questo nuovo punto di riferimento. Dividere l’immagine in 16 celle uguali (4×4), la soluzione è che ogni cella cambia in una forma specifica e tutti questi nuovi moduli possono essere uniti per ottenere una nuova immagine delle stesse dimensioni dell’originale. Quanto sopra può essere ottenuto utilizzando la trasformazione bilineale applicata a ciascuna cella.
La soluzione proposta è progettata per le immagini formate da una singola matrice, in modo che tale trasformazione non possa essere applicata a immagini in formato RGB.
sviluppo dell’esercizio.
in immagine 2 è sovrapposto a una rete blu, che deve cambiare rispetto alla trasformazione desiderata. Questa maglia ha 3 linee verticali e 3 linee orizzontali. La soluzione al problema originale è una soluzione generale, quindi solo l’immagine di esempio viene utilizzata in determinati momenti della descrizione in modo che la spiegazione sia più chiara.
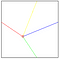
Figcaption> Image 3. A. Position PIXEL “1” B. Position Position “2”.
La prima cosa che è stata eseguita è di riferimento linee di riferimento. sopra, giù, verso destra e a sinistra del punto “x”. Sono le linee più brevi del punto “x” alle estremità dell’immagine, come visto nell’immagine 3.a. Le coordinate del punto “X” sono (PRX (1), PRY (1)).
Dopo aver localizzato le linee di riferimento, i punti di taglio di ciascuna riga della rete con queste linee di riferimento. È possibile che le linee di riferimento abbiano tagliato i punti con tre, con due, con una linea o nessuna linea di rete. Di seguito sono riportati i punti di intersezione per questo caso nell’immagine 4.

sono disegnati a quattro righe Riferimenti Nuovo per graficare la nuova maglia. Il punto Dove ti unisci a queste 4 nuove linee è il punto “o” le cui coordinate sono (PRX (2), PRIS (2)). In questo modo la parte gialla della linea del punto (PRX (2), PRY (2)) a Il punto (PRX (1), 1) Il 1 corrisponde alla prima riga di pixel dell’immagine, la parte blu della parte del PU NTO (PRX (2), PRY (2)) a Punto (X, PRIS (1)) La X corrisponde alla più recente colonna Pixel dell’immagine, la parte rossa della linea del punto (PRX (2), PRY (2 )) Al punto (1, PRIS (1)) il 1 corrisponde alla prima colonna pixel dell’immagine e la parte della linea verde del punto (PRX (2), PRRY (2)) al punto (PRX (1) , y) la colonna e corrisponde all’ultima riga di pixel dell’immagine, come mostrato nell’immagine 5.
Se si guarda, la posizione dei punti di intersezione, nella figura 3, deve cambiare in proporzione per cambiare il linea su cui si trovano. Dopo aver trovato il rapporto con cui cambiano e li trovano nella loro nuova posizione, otteniamo il seguente risultato: Immagine 6.

sul bordo dell’immagine 6 punti in cui le linee che compongono la rete sono posizionate da questi indicatori e i nuovi punti di intersezione sono Tracciare la nuova maglia. Nell’immagine 7 puoi vedere questo.
I valori che contano negli Stati Uniti nell’immagine 7 sono quelli che indicano i punti di intersezione delle linee discontinue.

Unendo questi punti di intersezione può graficare la nuova maglia. La nuova maglia viene utilizzata per il riferimento visivo, dal momento che per rendere la trasformazione Bilineale abbiamo solo bisogno dei punti di intersezione.

L’identificazione dell’intersezione dei punti viene eseguita con equazioni dritte, semplicemente l’attraversamento delle linee che generano i punti di interesse sono calcolati.
Ora che i nuovi punti della rete sono noti, possiamo eseguire la trasformazione bilineale di ciascuna cella. Esecuzione della trasformazione per la cella in cui si trova la maggior parte del viso Lena, è possibile spiegare il processo di trasformazione.

La trasformazione viene eseguita in una regione rettangolare che contiene la nuova regione, cioè una regione rettangolare in cui la regione è contenuta delimitata da k5, k8, k9 e k6. Prendendo come voce i punti che incorniciano ciascuna cellula e i nuovi punti che svolgono la trasformazione del Bilineo. Dopo la trasformazione otteniamo l’immagine 11 per la cella.

Se facciamo la trasformazione a tutte le cellule e sovrappongono le regioni ottenute il risultato dell’immagine 12.
Per evitare la sovrapposizione delle regioni, come vediamo nell’immagine 12, dobbiamo tagliare le regioni prima di sovrappostarle ciascuna. Se tagliiamo la cella dell’immagine 11 con il contorno K5, K8, K9 e K6 dell’immagine 9 otteniamo il risultato dell’immagine 13.

Dopo aver tagliato e sovrapponendo le regioni di taglio, il risultato dell’immagine è ottenuto.

Ho permesso ai bordi delle regioni di sovrapposizione per osservare Come è influenzata la rete.
Risultato di diversi punti.

Codice MATLAB
Con il seguente codice è possibile mettere attraverso la trasformazione passo dopo passo. Sicuro puoi ottimizzarlo.
clc; clear all; close all;im=imread(‘LenaMonoColor.bmp’);
=size(im);
a=round(x/4); %horizontal
b=round(y/4); %vertical
figure;imshow(im);
% =ginput(2);
% hold on;for k=0:5;
line(,);
line(,);
endim1=uint8(zeros(size(im)));
im2=uint8(zeros(size(im)));
im3=uint8(zeros(size(im)));
im4=uint8(zeros(size(im)));
im5=uint8(zeros(size(im)));
im6=uint8(zeros(size(im)));
im7=uint8(zeros(size(im)));
im8=uint8(zeros(size(im)));
im9=uint8(zeros(size(im)));
im10=uint8(zeros(size(im)));
im11=uint8(zeros(size(im)));
im12=uint8(zeros(size(im)));
im13=uint8(zeros(size(im)));
im14=uint8(zeros(size(im)));
im15=uint8(zeros(size(im)));
im16=uint8(zeros(size(im)));for xp=1:b;
for yp=1:a;
im1(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=a:a*2;
im2(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=2*a:3*a;
im3(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=3*a:4*a;
im4(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=1:a;
im5(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=a:2*a;
im6(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=2*a:3*a;
im7(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=3*a:4*a;
im8(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=1:a;
im9(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=a:2*a;
im10(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=2*a:3*a;
im11(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=3*a:4*a;
im12(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=1:a;
im13(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=a:2*a;
im14(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=2*a:3*a;
im15(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=3*a:4*a;
im16(xp,yp)=im(xp,yp);
end
endfigure,imshow(im1)
% figure,imshow(im2)
% figure,imshow(im3)
% figure,imshow(im4)
% figure,imshow(im5)
% figure,imshow(im6)
% figure,imshow(im7)
% figure,imshow(im8)
% figure,imshow(im9)
% figure,imshow(im10)
% figure,imshow(im11)
% figure,imshow(im12)
% figure,imshow(im13)
% figure,imshow(im14)
% figure,imshow(im15)
% figure,imshow(im16)
% line(px1,py1)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im21=uint8(zeros(size(im)));
for m=1:b+50;
for n=1:a+30;
im21(m,n)=im1(round(BP’*),round(AP’*));
end
end
figure, imshow(im21)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im22=uint8(zeros(size(im)));
for m=1:b+10;
for n=a:2*a;
im22(m,n)=im2(round(BP’*),round(AP’*));
end
end
figure, imshow(im22)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im25=uint8(zeros(size(im)));
for m=b+10:b*2;
for n=1:a+30;
im25(m,n)=im5(round(BP’*),round(AP’*));
end
end
figure, imshow(im25)X=’;
Y=’;
XP=’;
YP=’;
MP=;
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im26=uint8(zeros(size(im)));
for m=b:b*2;
for n=a:2*a;
im26(m,n)=im6(round(BP’*),round(AP’*));
end
end
figure, imshow(im26)im31=im21+im22+im3+im4+im25+im26+im7+im8+im9+im10+im11+im12+im13+im14+im15+im16;
figure, imshow(im31)
line(,)
line(,)
line(,)
line(,)
bilineal.m
Mostrando bilineal.m.