Dimostrazione di formule di area e volume utilizzando Integrali

Buono! In questa voce le formule che conosciamo tutti sull’area e il volume di corpi noti come cubetti, cerchi, sfere, piramidi …

Per questo sarà dimostrato, ovviamente, useremo l’integrazione numerica, Uno strumento matematico essenziale per qualsiasi tipo di calcolo che include una somma infinitesimale di valori diversi.

Per essere in grado di comprendere perfettamente alcuni calcoli esposti che devi sapere Almeno integrare in una variabile ed è altamente raccomandato di visitare questo articolo: doppio e triplo integrali. Modifiche delle variabili

Sommario

le formule

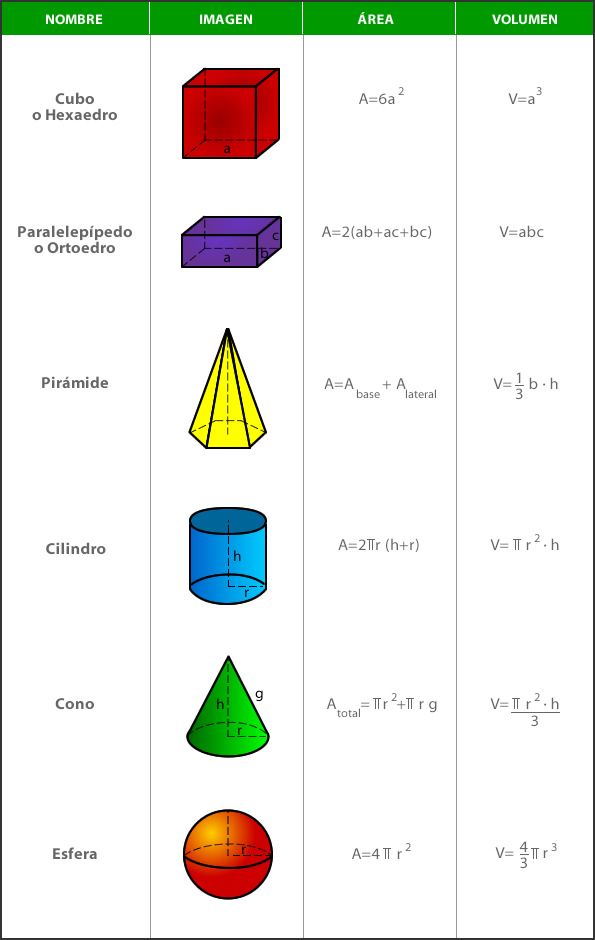
Per calcolare un’area o un volume, ciò che è fatto è calcolare il calcolo integrale (semplice, doppio, triplo, curvilineo, superficie …) della funzione costante F = 1 sul recinto le cui dimensioni Vogliamo calcolare.

Parallelepípedo

Impiegato Integrali per questo corpo geometrico equivale a uccidere mosche a cannone; Tuttavia, come prima utilità di base di doppio e triplo integrali calcoleremo il suo volume

Volume

Il nostro involucro di integrazione è un parallelepipedo dei lati A, B e C. Pertanto, l’integrale rimane:

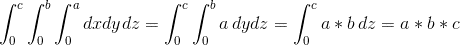
cerchio

Tutti conoscono le sue formule:

$2 \ PI R$ e $\ PI R 2$ . Ma, come deducano?

Prima di tutto, dobbiamo sapere che se vogliamo rappresentare graficamente una funzione di circonferenza, non può essere rappresentato così facilmente dal modulo e = f (x) poiché non è iniettivo, Sta dicendo, per un valore X, vengono visualizzati 2 valori e (la formula generale per un raggio ry centrata sull’origine della coordinata è

<2} = r 2

. (Nel caso di voler dipingere un cerchio, basta cambiare = da < =). Pertanto, viene utilizzata la parametrizzazione:

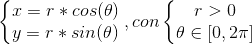
Dimostrazione di formule e volume di area tramite integrali 2

Di chi deve determinare Jacobiano, per il cambio di variabili è: r

Se vuoi saperne di più sulla circonferenza e su come si ottiene la tua formula in modo più dettagliato, questo è il tuo articolo

Qui puoi giocare un po ‘con il Equazione della circonferenza: collegamento a DESMOS

perimetro

the r ECCTO è quel “filo” che costituisce il bordo esterno del cerchio. Pertanto, la curva parametrizzata di detto filo è:

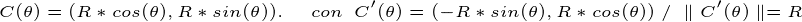
dimostrazione di formule di area e volume da parte integrali 3

Calcolo del curvilineo integrale sulla funzione costante f = 1 — >

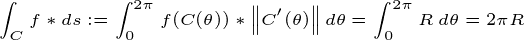
Area

Per calcolare L’area, è sufficiente calcolare l’integrale sul contenitore delimitato dalla circonferenza. Per facilitare i calcoli che passiamo dalle coordinate cartesiane (x, y) a Polares (R,

$\ theta$ ) usando il jacobiano r per il cambio della variabile. $\ INT_ {S} DXDY = \ INT_ {0} ^ {} {0} ^ {} {0} {0}} {2 \ PI} R DRD \ Theta = 2 * \ PI \ INT_ {0} RY R DR = 2 * \ PI * \ FRAC {R 2} {2} = \ PI * R 2$

SPHER

Il caso della sfera Le sue formule sono alquanto più sconosciute.

$\ frac {4} {3} * \ pi * r 3$ per volume e $4 * \ pi * r 2$ per l’area della sua superficie.

Come con il cerchio, useremo altre coordinate, le coordinate sferiche. L’equazione della sfera in cartesianas è

la parametrizzazione it:

$\ sinistra \ {\ begin {matrice} x = r * sen (\ theta) * cos (\ phi) \\ y = r * sen (\ theta) * sen (\ phi) \\ z = R * cos (\ theta) \ end {matrice} \ destra$ , con $\ sinistra \ {\ begg {matrice} 0 \ leq r \ leq r \\ 0 \ leq \ Phi \ Leq 2 \ leq \ pi \ end {matrice} \ destra$

il cui jacobian è

$r 2 * sen (\ theta)$

Qui puoi giocare un po ‘con l’equazione della sfera: immettere GeoGebra 3D e incolla questo nell’editore: Superficie (R * Sen (U) * Cos (V), R * Sen (U) * Sen (V) , R * cos (u), u, 0, pi, v, 0,2pi)

area

Per calcolare l’area, è sufficiente per calcolare la gamma di viaggio la parametrizzazione con r = r.Calcoliamo l’integrale facendo il cambio di variabile con il Jacobian.

$\ INT \ INT_ {S} DXDY = \ INT_ {0} ^ {\ PI} {0} {0} ^ {2 \ pi} r 2 * sen (\ theta) d \ d \ phi = 2 * \ pi * r 2 * \ int_ {0} ^ {\ pi} sen (\ theta) d \ theta = 4 * \ PI * R 2$

Volume

Per il volume calcoliamo l’integrale dell’intero contenitore

usando le variabili $DRD \ Theta D \ phi$ $\ int / int_ {v} dxdydz = \ int_ {0} ^ {\ pi}} int_ {0} \ {r} \ int_ {0} ^ {2 \ PI} R 2 * SEN (\ PI} R 2 * SEN (\ theta) D \ theta d \ phi = 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ° R 2 * SEN (\ theta) D \ theta DR \ RightArrow$ $\ Right Docka 2 * \ PI * \ int_ {0} ^ {\ PI} \ INT_ {0} ° R 2 * sen (\ theta) d \ theta dr = \ frac {2} {3} * \ pi * r 3 \ int_ {0} ^ {\ pi} sen (\ theta) d \ theta = \ frac {4 } {3} * \ pi * r 3$

Piramide

Il modo per calcolare il volume di una piramide è identico a quello di un parallelepipedo; La complicazione è stabilire i limiti di integrazione (il contenitore).

Tirare la logica, la coordinata Z sarà gratuita, variabile da 0 a h. Le coordinate XEY dipenderà dalla coordinata Z per quanto riguarda i valori massimi che prendono, a partire da -B / 2 AB / 2 al massimo alla base e prendendo come un singolo valore 0 quando Z = H (PIRAMIDA PICK). Sulla base di questo approccio, prendiamo i limiti delle variabili:

$\ SINISTRA {\ Begin {Matrix} - \ frac {b} {2} * (1- \ frac {z } {H) \ leq x ≤ \ frac {b} {2} * (1- \ frac {z} {h) \\ - \ frac {b} {2} * (1- \ frac {z} {h ) \ leq e \ leq \ frac {b} {2} * (1- \ frac {z} {h) \\ \ leq z \ leq h \ end {matrice} \ destro$

volume

Calcolamo l’integrale sul recinto DXDYDZ

$V = \ iiint_ {v} dxdydz = \ int_ {0} ^} \ int_ {- \ frac {b } {2} * (1- \ frac {z} {h)} ^ \ frac {B} {2} * (1- \ frac {z} {h)} \ int_ {- \ frac {b} {2 } * (1- \ frac {z} {h)} ^ \ frac {b} {2} * (1- \ frac {z} {h)} d e dx = \ int_ {0} ^ {h} b 2 * (1- \ frac {z} {h) 2 dz = \ reapyarrow$

cono

Il cono è molto simile alla piramide. Tuttavia, dobbiamo utilizzare le coordinate polari per parametrizzare correttamente la base circolare. Utilizzeremo le variabili

$\ z, \ r \ y \ \ theta$ . A seguito di una detrazione simile alla piramide che abbiamo lasciato: $\ sinistra \ {\ bein {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r * (1- \ frac {z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ line \ leq 2 \ pi \ end {matrice} \ destra$

Volume

Calcolamo l’integrale sul contenitore DixyDz e Facciamo il cambio di variabile per Polar con JACOBIANO R

$V = \ IIINT_ {V} DXDYDZ = \ INT_ {0} ^ \ INT_ {0} Q (1- \ frac { Z} {h)} \ int_ {0} ^ {2 \ PI} r \ Dzdrd \ theta = \ pi ^ int_ {0} ^ {h} r$ * (1- \ crac {z} {h) 2 = \ Right Dochaprow

$= \ raggi \ pi * r 2 \ int_ {0} ^ ^ {h} (1+ \ frac {z 2} {h 2} - \ frac {2Z} {h) = \ PI * R 2 * 0 ^ {H} = \ PI * R ^ {2} * = \ PI * R 2 * \ FRAC {H} {3}$

che, come previsto, proprio come la piramide la sua formula è

$area \ de \ \ base * \ frac {altezza} {3}$

cilindro

Il cilindro è forse la figura più intuitiva quando si calcola l’area della superficie e il suo volume. Nonostante sia ovvio, mostreremo come il tuo volume potrebbe essere calcolato in modo integrale (essendo, chiaramente, area di base * altezza) in modo che il funzionamento di tripli integrali sia meglio compreso.

Utilizzeremo Le variabili

$\ z, \ r \ y \ \ \ theta$ tali: $\ sinistra \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r \\ \ pi \ end {matrice} \ destra$

Volume

Calcolamo l’integrale sul recinto DXDYDZ e apportare il cambio di variabile per polare con JACOBIANO R

$V = \ iiint_ {v dxdydz = \ int_ {0} ^ {h} {0} {0}} {R} \} int_ {0} 2 r \ dzdrd \ theta = 2 \ pi \ int_ {0} ^ {h} \} {0} ° r \ DZDR = \ RightArrow$ $\ Right Direct = \ PI * R 2 * \ INT_ {0} ^ H DZ = \ PI * R 2 * H$

Dimostrazione di formule di area e volume via integrali

le formule

Parallelepípedo

Volume

cerchio

perimetro

Area

SPHER

area

Volume

Piramide

volume

cono

Volume

cilindro

Volume

Lascia un commento Annulla risposta