Procesamento de imaxes. Transformación bilineal. [MATLAB]

A visión é o sentido polo cal obtemos a maior información sobre o noso contorno .. A interpretación do noso cerebro, en función da información que recibe dos ollos, está fortemente influenciada pola experiencia; Isto ás veces leva a facer erros de apreciación. Ao longo do tempo da túa vida, e especialmente nas últimas idades, un individuo categorizado, xeneraliza e caracteriza os elementos do teu contorno para tomar decisións rápidamente. As persoas que teñen deficiencias no seu sentido de vista poden corrixir ou reducir os defectos deste por medio de lentes, isto é posible se falamos de problemas de aproximación por exemplo. Co desenvolvemento da adquisición de imaxes a través de ferramentas tecnolóxicas, a necesidade de corrixir estas imaxes tamén xurdiu para que a súa posterior interpretación sexa certa. Se un dispositivo de adquisición de imaxes ofrece imaxes con defectos de foco, esta deficiencia pode ser corrixida engadindo lentes ao dispositivo. A perspectiva é un aspecto importante ao interpretar unha imaxe, a fundación deste aspecto está na experiencia, xa que é como aprendemos a estimar medidas, posicións, velocidades, etc. Unha interpretación precisa da imaxe obtida pódese conseguir se as características do obxecto que contiñan son coñecidas polo individuo que o analiza. Existe a importancia das proporcións da imaxe, con respecto á realidade, son congruentes. Tamén usamos a perspectiva de suxerir unha idea a un individuo ou persuadirlo e alí atopamos coraxe cando se trata de modificar as proporcións dos elementos dunha imaxe. Cando a imaxe adquirida non corresponde ao que queremos visualizar podemos facer unha modificación da imaxe para que sexa máis cómodo.

Para modificar unha imaxe, coordinar transformacións dos píxeles e modificacións no brillo Da imaxe, este último conséguese con técnicas de interpolación de brillo. Cambiar as proporcións da imaxe pódese entender cunha acción análoga: se temos unha superficie de xeo e expandir esta superficie con calor, obteremos unha superficie de vapor e haberá rexións baleiras sobre a devandita superficie. O mesmo efecto ocorre nas imaxes e para compensar este defecto, úsanse técnicas de interpolación; Con estas técnicas asumimos valores a lugares baleiros para que a imaxe sexa apreciada uniforme, isto está relacionado coa resolución da imaxe. A forma en que afectamos a xeometría da imaxe está baseada en técnicas de transformación xeométrica. Se queremos mover a imaxe, cambiar as proporcións de base e de altura, xirar ou deslizarse, podemos realizar a transformación lineal relacionada. Se desexa cambiar a xeometría da imaxe sen preservar o paralelismo entre as liñas opostas do contorno da imaxe, podemos usar unha transformación bilineal ou unha transformación de perspectiva. Esta transformación usa 4 puntos de referencia e 4 puntos de transformación para definir a función de transformación.

O obxectivo desta práctica é modificar unha imaxe de altura “e” e base “x”. A imaxe será modificada a partir de dous puntos da imaxe. Para formular O problema e describe a solución proposta, usarase unha imaxe de exemplo. Desexa modificar a imaxe 2, porque este píxel marcado cun “X” vermello está seleccionado e a posición que se desexa levar cun “ou” roj A, para este caso. O punto de referencia “X” terá as coordenadas (PRX (1), PRY (1)). O punto de referencia “ou” terá as coordenadas (PRX (2), Pry (2)). O primeiro elemento da nomenclatura anterior corresponde á posición sobre o eixe horizontal e o segundo elemento corresponde á posición sobre o eixe vertical. Debe ter en conta que para localizar estes puntos, o punto de referencia punto está na esquina superior esquerda da imaxe.

A transformación lineal será utilizada para modificar unha imaxe baseada na selección de dous píxeles de a imaxe. En primeiro lugar, o píxel “1” está seleccionado e posteriormente o píxel “2”.A imaxe cambiará con respecto a estes dous puntos de referencia; Quere mover o píxel “1” á posición de píxeles “2”, toda a imaxe debe cambiar para acomodar este novo punto de referencia. Dividindo a imaxe en 16 celas iguais (4×4), a solución é que cada célula cambia a unha forma específica e toda esa nova forma pode unirse a unha nova imaxe das mesmas dimensións do orixinal. O anterior pódese conseguir utilizando a transformación bilineal aplicada a cada cela.

A solución proposta está deseñada para imaxes formadas por unha única matriz, de xeito que esa transformación non se pode aplicar a imaxes en formato RGB por exemplo.

Desenvolvemento de exercicios.

Na imaxe 2 está superposta por unha malla azul, que debe cambiar con respecto á transformación desexada. Esta malla ten 3 liñas verticais e 3 liñas horizontais. A solución ao problema orixinal é unha solución xeral, polo que só a imaxe de exemplo úsase en determinados momentos da descrición para que a explicación sexa máis clara.

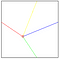
O primeiro que se fai é localizar as liñas de referencia Por riba, abaixo, cara á dereita e á esquerda do punto “X”. Son as liñas máis curtas desde o punto “X” ata os extremos da imaxe, como se ve na imaxe 3.a. As coordenadas do punto “X” son (PRX (1), PRY (1)).

Despois de localizar as liñas de referencia, os puntos de corte de cada liña da malla con estas liñas de referencia. É posible que as liñas de referencia corten puntos con tres, con dúas, cunha ou ningunha liña de malla. Abaixo amósanse os puntos de intersección para este caso na imaxe 4.

Drawn Four Lines Referen New to Graph The New Mesh. O punto onde se unen a estas 4 novas liñas é o punto “ou” cuxas coordenadas son (PRX (2), PRY (2)). Deste xeito a liña amarela parte do punto (PRX (2), Pry (2)) a O punto (PRX (1), 1) O 1 corresponde á primeira fila de píxel da imaxe, a liña azul da PU Nto (PRX (2), Pry (2)) a punto (X, Pry (1)) O X corresponde á última columna de píxeles da imaxe, a parte vermella parte do punto (PRX (2), Pry (2 )) A punto (1, Pry (1)) O 1 corresponde á primeira columna de píxeles da imaxe e da liña verde do punto (PRX (2), PRRY (2)) ata o punto (PRX (1) , y) a columna e corresponde á última fila de píxeles da imaxe, como se mostra na imaxe 5.

Se ollas, a localización dos puntos de intersección, na Figura 3, debe cambiar de proporción para cambiar a liña na que se atopan. Despois de atopar a relación coa que cambian e localizalos na súa nova posición, obtemos o seguinte resultado: Imaxe 6.

No bordo da imaxe 6 puntos onde se colocan as liñas que compoñen a malla destes indicadores e os novos puntos de intersección son trazou a nova malla. Na imaxe 7 pode ver isto.

Os valores que nos importan na imaxe 7 son aqueles que indican os puntos de intersección das liñas discontinuas.

Unir estes puntos de intersección pode gráfica a nova malla. A nova malla utilízase para a referencia visual, xa que para facer a transformación bilineal só necesitamos os puntos de intersección.

A identificación da intersección dos puntos faise con ecuacións rectas, simplemente calcúlase o cruzamento das liñas que xeran os puntos de interese.

Agora que os novos puntos da malla son coñecidos, podemos realizar a transformación bilineal de cada cela. Realizando a transformación para a cela onde se atopa a maior parte da cara de Lena, pódese explicar o proceso de transformación.

A transformación lévase a cabo nunha rexión rectangular que contén a nova rexión, é dicir, unha rexión rectangular onde a rexión está delimitada por k5, k8, k9 e k6. Tomando como entrada os puntos que enmarcan cada cela e os novos puntos que realizamos a transformación bilineal. Despois da transformación obtemos a imaxe 11 para a célula.