intersección
Sean \ (s) e \ (t \) subespacios do mesmo espazo vectorial \ (( V \). Definimos a intersección do seguinte xeito:
\ (\ cap t = \ esquerda {{V \ in v \ ;: \; V \ in s \ ; \; \ Wedge \; \; V \ in t} \ dereito \} \; \) Intersección de subespacio
propiedade
(s \ cap t) é subespacio de \ (v)
demostración
1. \ ({0_v} \ in s \ wedge {0_v} \ in t \ rightarrow {0_v} \ in s \ cap t \)
2. Considerar \ (u, \; v \; \ in \; · \)
\ \\]
de e dedúcese isto \ (U + \; V \; \ \ \; \)
3. Deixamos o lector polo lector para demostrar:
\
exemplo 1
Visto a subspacios de \ ({\ mathbb {R} ^ 3} \ ):
\
\
Buscar \ (s \ cap t \).
resolución
por definición \ (s \ cap t \) é un conxunto que estará formado polos vectores que pertencen a \ (s \) e \ (t \). É dicir, aqueles vectores que satisfán as ecuacións de \ (s \) e as de \ (t \):
\
trátase de Unha recta definida como intersección de dous planos. Unha base da recta é un vector de director.
xeométricamente podemos buscar o director de vectores como o produto vectorial dos vectores normais dos planos:
\
\
entón \ (\ esquerda \ \ \; \ esquerda ({3, – 2,1} dereita) \;} \ Right \} \) é unha base de \ (s \ cap t \).
Outra forma de resolver é buscar a solución de solución do sistema:
\
\
e despois chegamos a iso \ (\ esquerda \ \ \; \ esquerda ( {3, – 2.1} \ right) \;} \ right \} \) é unha base de \ (s \ cap t \).
exemplo 2
Sexa o sub -Sites de \ ({\ mathbb {R} ^ {2 × 2}} \):
\
\
Buscar \ (s \ cap t \).
resolución
A intersección do subespacio está formada polos vectores que verifican as ecuacións de devanditos subespais.
Que ten que cumprir unha matriz para pertencer a \ (s)?
\
Que ten que cumprir unha matriz para pertencer a \ (t)?
ten que ser capaz de ser escrito como combinación lineal de: \ (\ esquerda ({\ begin {matry} {* {20} {C}} 1 & 0 \\ 2 & {- 1} end {array}} \ right) \; e \ esquerda ({{{20} {C}} 1 & 0 \\ 1 & 0 end {array}} \ right) \)
Atopamos as ecuacións subespaciais \ (t \):
\
\
\
\
Agora consideramos que as matrices de \ (s \ cap t \; \) deben cumprir as ecuacións de \ (s \) e aqueles de \ (t \):
\
que é:
\
A continuación, as matrices de \ (s \ cap t \) son a forma:
\
e unha base de \ (s \ Cap T \) en:
\
Hai un método máis curto alternativo para atopar unha base de \ (s \ c AP T \) Sen a necesidade de obter as ecuacións de \ (t \), como veremos a continuación.
Escribimos unha matriz de \ (t \) como unha combinación lineal dos vectores que xeran É:
pero ademais, deben cumprirse as ecuacións de \ (s) que establecen que \ (C = B) debería cumprirse. Entón:
\
Polo tanto, unha matriz de \ (s \ cap t \) é:
\
Sume de subespacios
Dado \ (s, \; t \) subespacios de \ (V), a suma do seguinte xeito:
\ (S + T = \ LEFT \ {{V \ in V \ ;: \; \; v = {v_1} + {v_2} \; \;, \; \; con \; \; {v_1} \ in s \;, \; \; {v_2} \ in t} \ rightt \) suma de subespacios
Propiedade: \ (S + T \) é un subespacio de espazo vectorial \ (V).
Deixamos a demostración do lector.
Se sabemos conxuntos e Xeradores de T, podemos atopar xeradores de sumas:
\ (s = xene \ esquerda {{{{{{{v_1}, {v_2}, \ Ldots, {v_q}} \ right \} \) e \ (t = xene \ esquerda {{{{w_1}, {w_2}, \ lDOTS, {w_r}} \ right \} \) \ (\; \ rightarrow \; S + t = gen \ esquerda {{{v_1}, {v_2}, \ lDOTS {v_q}, {w_1}, {w_2}, \ lDOTS, {w_r}} \ right \} \)
Para atopar a suma é habitual buscar as bases de \ (s \) e \ (t \). Dado que as bases son conxuntos de xeración de Li, se sabemos unha base de cada subpacio, podemos obter un conxunto de xeradores de conxunto:
Dada a bases:
\ ({b_s} = \ esquerda \ {{{v_1}, {v_2, \ ldots, {v_q}} \ right \} \) e \ ({b_t} = \ esquerda {{{w_1}, {W_2}, \ lDots, {w_r}} \ right \} \)
Resultados:
\ (\ esquerda \ {{{{ V_1}, \ lDOTS, {V_Q}, {W_1}, \ lDOTS, {W_R}} \ right \} \) Summerator xerador.
Observación: un conxunto de xeradores da suma obtense, pero non sempre é lineal independente.
- Se vostede é li, atopamos unha base de a suma.
- Se é ld, podemos extraer unha base da suma eliminando os vectores “Sobran”.
exemplo 1
Dado os seguintes subespazos \ (v = {\ mathbb {R} ^ 3} \):
\
\
Estamos interesados en atopar \ (s + t \).
imos buscar unha base de \ (s \). Por iso, na ecuación, claro unha variable:
\
Agora establecemos un vector xenérico:
\
\
Buscar unha base de \ (T \). Para iso, na ecuación, claro unha variable:
\
Agora establecemos un vector xenérico:
\
entón
\
\
Sabemos que todo o conxunto de máis de 3 vectores en \ ({\ mathbb {R} ^ 3} \) é dependente linealmente, xa que a dimensión de \ ({\ mathbb {R} ^ 3 } \) En 3. Como podemos extraer unha base da suma?
Poderiamos reunir unha matriz con estes 4 vectores e levala ao formulario escalonado. Ou se non, como o espazo é \ ({\ mathbb {R} ^ 3}), podemos pensar xeométricamente:
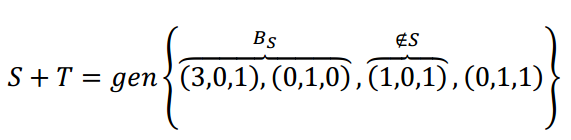
Como \ (\ esquerda ({1,0,1} \ right) \) non verifica a ecuación do avión S, os 3 primeiros vectores non son coplanar e, polo tanto, forman unha base de \ (\ mathbb {r} ^ 3 \) .. Podemos borrar \ (\ esquerda ({0,1,1} \ right) \) \) porque é unha combinación lineal da devandita base.
Polo tanto: \ (b = \ esquerda {{\ esquerda ({3.0 .1} \ right), \ esquerda ({0,1.0} dereita), \ esquerda ({1,0,1} \ right)} \ right \} \) é a base de \ (s + t \) e é a base de \ (\ mathbb {r} ^ 3 \).
Neste caso, como \ (s + t \; \) é un subespacio de dimensión \ ({r ^ 3} \) 3 , podemos afirmar que:
\
xeneralización:
\ (S \) subespazo \ (V) e \ (\ dim \ á esquerda (s \ right) = \ Dim \ á esquerda (V \ right) \ rightarrow s = V)
Exemplo 2
Dado os seguintes sub-paquetes de \ (v = {\ mathbb {R} ^ 4} \):
\
\
Buscar base e dimensión de \ ({S_1} + {S_2} \; \).
Resolución
\
\
\
\
\
Como vimos, a método para analizar se s En Li ou LD, consiste en reunir unha matriz cos vectores como filas e levala á súa forma escalonada. Por comodidade imos poñer os vectores na seguinte orde:
\ (\ esquerda ({\ begin {array} {20} {C}} 1 & {- 1} & 0 & 1 \\ 1 & 0 & {- 1} & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 end {array}} \ right) \)
\ (\ mathop \ a {f_2} {f_1}} \ esquerda ({\ begin {array} {* {20}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 1 & 0 IV id = “26A2980253” 0 \\ 0 & 0 1 & 0 \ end {array} } \ right) \) /p>
\ (\ mathop \ to} – {f_2} {f_3} – {f_2}} esquerda ({\ begin {array} {* {20} {C} } 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ Mathop \ to {f_4 _4} {f_4} – {f_3}} \ esquerda ({\ begin {array} {* {20}} 1 & {- 1} & 0 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 end {array}} \ right) \)
a matriz ARCA Lonada ten 3 filas de Li (o seu alcance é 3), entón podemos afirmar que o tamaño de \ (S + T \) é 3.
A medida que a última fila foi anulada, o vector \ (\ esquerda ({{0.0,0} \ right) \) é unha combinación lineal dos outros tres, polo tanto, unha base de \ (s + t \) é: \ ({B_ {S + T}} = \ esquerda {{\ esquerda ({1, – 1,0,1} →, \ esquerda ({0,1,0, 0} → esquerda ( {1.0, – 1.1} \ right)} \ right \} \).
Lembre que as filas da matriz escalonada compoñen outra base da suma:
\
Suma directa
A cantidade de dous subespacios é directo se e só se a intersección dos subespacios é o vector cero.
Cando a suma é directa está escrita:
\
exemplos en \ ({\ rm {v} = {\ mathbb {R} ^ 3} \)
A continuación consideraremos diferentes sumas de suma de subespazos en \ ({\ mathbb {R} ^ 3} \ ).
dúas rectas
Un posible caso de suma de dúas subespacios en \ ({\ mathbb {R} ^ 3} \) é o de dúas rectas rectas que se cortan :
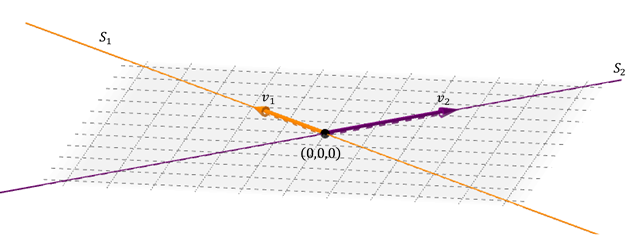
L. Os dous vectores rectos de Li xeran un mapa: o que contén ambas rectas. A suma é directa porque a intersección entre as liñas é o vector nulo.
\
\ (( {S_1} \ opus {s_2} = s \) onde \ (s \) é o avión que contén as dúas liñas
dous planos que son cortados
outro caso posible de suma de dous subespazos en \ ({\ mathbb {R} ^ 3} \) é o debuxo de dous debuxos: 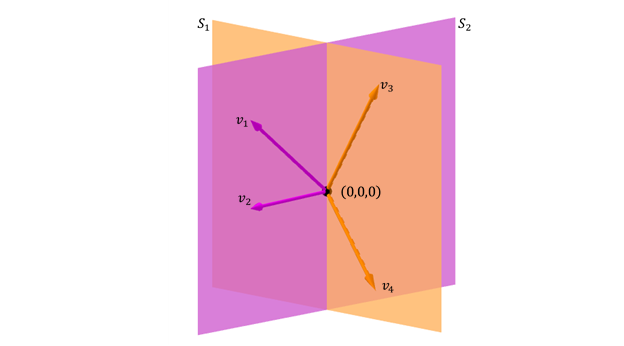
\}} = xene \ {{{\; {v_1}, {v_2}, {v_3}} \ rightt \} \]
a suma do Subspacios é \ ({\ Mathbb {R} ^ 3} \) Pero non é unha suma directa porque a intersección non é o vector cero:
\
un avión e unha directa incluída no avión
Outro caso posible de dous subespactos en \ ({\ mathbb {R} ^ 3} \) é o dun piso e un dereito incluído en o avión. 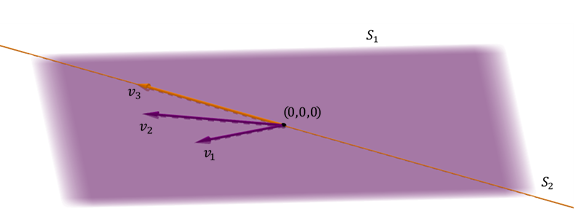
\
O mesmo plano obtense e a suma non é directa Porque a intersección non é igual ao vector cero.
un avión e un dereito non incluído no avión
Outro caso posible de suma de dous sub-appracios en \ ({\ \ MathBB {R} ^ 3} \) é o dun avión e un dereito non incluído no avión. 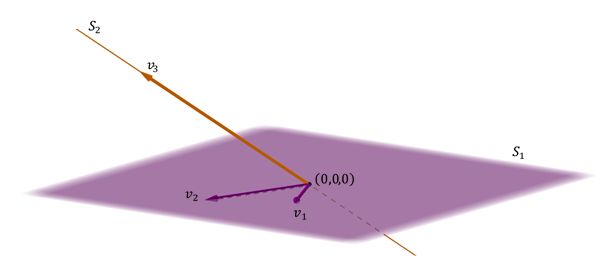
\
xérase \ ({\ mathbb {R} ^ 3} \ ) Porque o director de vectores da liña non está afrontando os vectores do avión, e tamén é directo porque a intersección é Null Vector:
\
Observación: no último caso, A unión das bases dos dous subespaces forma unha base de todo espazo. Neste caso, cada vector de \ ({\ mathbb {r} ^ 3} \) pode expresarse de forma única como suma dun vector de \ (_1} \) e outro de \ ({s_2} \).
Exercicio para lector 3
dados \ ({s_1} = gen \ left \ {{\ esquerda ({1,2,1} dereita), \ \ esquerda ({{ 0,2,0} \ right)} \ right \} \) e \ ({s_2} = \ esquerda {\ esquerda ({x, y, z} dereita): \; \; \; x + y = y – Kz = 0} \ right \} \),
a) Atopar os valores de \ (k \) para os que \ ({s_1} \ opus {s_1} = {\ mathbb {R} ^ 3} \).
b) para \ (k = 0 \), verifique que \ (v = \ esquerda ({3,2,2,2 \ right) \) pode expresarse un xeito único como suma dun vector \ ({v_1} \ in {s_1} \) e un de \ ({v_2} \ in {s_2} \).
exercicio para lector 4
son os sub-appracios de \ ({\ mathbb {R} ^ 4} \):
\ (s = xene \ esquerda {\ esquerda ({1,1,1, 1} \ right), \ \ á esquerda ({0,1,0,1} \ right)} \ right \} \) e \ (t = \ esquerda \ {{\ esquerda ({x, y, z, t} → : \; \; \;, \; \; xz + t = 0} \ right \} \)
Cal das seguintes afirmacións é correcta? Xustificar.
- \ (s \ opus t = {\ mathbb {r} ^ 4} \)
- \ (s + t = {\ mathbb {R} ^ 4} \)
- \ (s + t = w \; \; \; e \; \ dim \ á esquerda (w \ right) = 3 \)
- \ (s \ OPlus T = w \) e \ (\ dim \ á esquerda (w \ dereito) = 3 \)
Teorema da dimensión da suma
Si \ ({{ S_1} \) e \ ({s_2} \) son sub-espazos dun espazo vectorial \ (V) (dimensión finita), entón:
\
No caso particular que a suma é directa, como \ ({s_1} → {_2} = \ esquerda {{{{{0_v}} \ right \} \ ), é:
\
exemplo
Dado a subespacios \ ({P_2} \):
\
\
Buscar bases dos subespais e da intersección
resolución
Atopamos unha base de \ ({s_1} \):
\
entón son os polinomios do formulario:
\
entón unha base de \ ({s_1} \) é:
\
Atopamos unha base de \ ({s _2} \):
\
entón son os polinomios do formulario:
\
\
para buscar \ ({s_1} · \ cap {s_2} \) Debemos considerar que as ecuacións de \ ({S_1} \) e tamén aqueles de \ (_2} \):
\
Os polinomios estarán no formulario:
\
entón:
\
Teña en conta que, como sabemos as dimensións de \ (_1} \), \ ({s_2} \) e \ ({s_1} · {s_2} \), podemos calcular a dimensión de \ ({s_1} + {s_2} \):
\
Pero o único subespacio de \ ({P_2} \) con dimensión 3 é \ ({P_2} \) .. Entón: \ ({S_1} + {S_2} = {P_2} \).
Exercicio para o lector 5
Dada a subespacios de \ ({\ mathbb {R} ^ {2 \ veces 2}} \):
\
\
a) atopar bases de \ ({w_1} \) e \ ({w_2} \ ({w_1} → _2} \).
c) sen atopar \ ({w_1} + {w_2} \) analizar a validez da seguinte afirmación:
\
d) Propoñer unha base de \ ({\ mathbb {R} 2} \) formada por matrices simétricas e anti-inmemétricas e expresar a matriz
\
como unha matriz simétrica máis un produto interno.
Produto interno
Na primeira unidade que nós viu o produto escalar entre os vectores e as súas aplicacións á xeometría. Nesta sección propoñemos xeneralizar esta operación a outros espazos vectoriais, definindo a noción xeral do produto interno das propiedades do produto escalar.
Definición: un produto interno nun espazo vectorial real \ (V) é unha operación que atribúe a cada torque vectorial \ (u \) e \ (v) de \ (v) un número real \ (u \; V \) como as seguintes propiedades son verificadas (para todo vector \ (u, \; v, \; w) de \ (V) e todo escalar \ (\ alpha \)): 1. \ (U \ cdot v = v \ cdot u \)
2. \ (u \ cdot \ á esquerda ({v + w} \ right) = \ esquerda ({u \ cdot v} \ right) + \ loft ({u \ cdot w} \ right) \)
3. \ (α u \ cdot v = \ alpha \ á esquerda ({u \ cdot v} \ right) \)
4. \ (UU ≥ \ GE 0 \; \; uu = 0 \; \; \; \ leftrightarrow \; \; \; \; u = {0_v} \) /p>
it é posible definir diferentes produtos internos en calquera espazo vectorial (mentres que estas propiedades son verificadas). No noso tema, só traballaremos co produto interno canónico en \ ({\ mathbb {R} ^ n} \), que é a propagación do produto a escala:
\ (\ esquerda ({{x_1}, {x_2} ldots, {x_n}} dereita). \ esquerda ({{Y_1}, {Y_2}, \ lDOTS, {Y_N}} \ dereito) = {x_1} {y_1} + {x_2} {y_2} + ldots {x_n} {y_n} \) produto interno canon en \ (\ mathbb {r} ^ n \)
Esta definición permítenos ampliar o concepto de ortogonalidade a \ ({\ mathbb {R} ^ n} \):
\ (u \ bot v \; \; \ \ leftrightarrow \; \; uv = 0 \) condición de ortogonalidade
exemplo
imos realizar o produto interno de \ ({ \ Mathbb {r} ^ 4} \):
\
\
como \ (UV = 0) entón \ (u \) e \ (v) son ortogonales. \ (\; \)
complemento ortogonal dun subespacio
Deixe \ (s) subespacio de \ (V \) (espazo vectorial con produto interno).
O complemento ortogonal de \ (s \), que denotar como \ ({s \ bo T} \), é o conxunto de vectores de \ (V) que son ortogonales a cada un dos vectores de \ (s \):
Propiedade: \ ({{^ \ BOT} \) é un subespacio de \ (V).
1. \ ({0_v} \) pertence a \ ({S \ BOT} \) como \ ({0_v} .w \; = \; 0 \) para todo \ (w \) de \ (s)
2. Sean \ (u, v \ in {s ^ \ BOT} → 0 \ wedge VW \; = \; 0 \; \; \; \ Fortall w \ in s \ rightarrow \ esquerda ({U + V} \ right) .w \; = \; uw \; + \; v.W \; = \; 0 \)
Polo tanto \ (U + V) está en \ ({S ^ \ BOT} \)
3. Si \ (u ~ {s ^ \ BOT} → {^ ^ \ BOT} \). Por que?
exemplo 1
mar \ (s = \ esquerda \ {\ esquerda ({x, y, z} dereita) \ en {\ mathbb {R} ^ 3 } \; | \; 2x + 3 e – z = 0} \ right \} \). Atopar \ ({S ^ \ BOT} \).
resolución
Temos que buscar \ ({\ mathbb {R} ^ 3} \) que son perpendiculares a todos Vectores dese avión.
Primeiro buscamos unha base de \ (s \), por exemplo:
\
Para atopar o complemento ortogonal, buscamos todos os vectores \ (\ esquerda ({x, y, z} dereita) \) que son ortogonales a \ (\ esquerda ({- 1 ,,1}) \ right) \ ) Xa (\ esquerda ({0,1,3} \ right) \).
Un sistema de ecuacións que definen o suplemento ortogonal:
\
\
¿Que é unha base de subespacio \ ({s ^ \ BOT} \)?
\
A base é un vector perpendicular para o avión \ (s \). Polo tanto, o complemento ortogonal dun avión que pasa pola orixe é a liña perpendicular que pasa pola orixe.
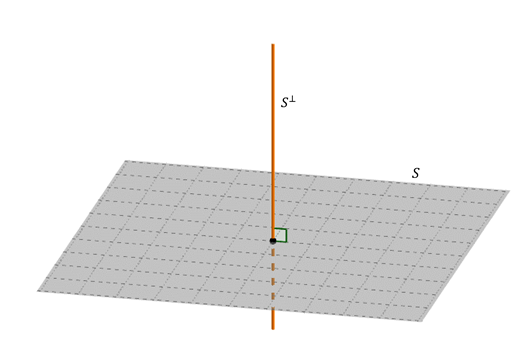
Si \ (s \) é unha liña que pasa pola fonte: cal é o seu suplemento ortogonal?
exercicio para lector 6
Para xustificar o procedemento que usamos para atopar as ecuacións de \ (^ \ BOT} \), pedimos que demostren a seguinte propiedade:
Sean \ (u, \; V, \ ; W \) vectores de \ ({\ mathbb {r} ^ n} \).
Si \ (w) é ortogonal a \ (u \) xa \ (V), entón é ortogonal a calquera combinación lineal de \ (u \) e \ (v).
exemplo 2
Dado o seguinte subespacio \ ({\ mathbb {R} ^ 4} \ ):
\
base de halle e dimensión do complemento ortogonal.
resolución
Temos que buscar os vectores de \ ({\ mathbb {R} ^ 4} \) que son ortogonales aos \ (s \) vectores.
Atopamos unha base de \ (s \ ):
\
\
Agora estamos a buscar \ ( \ esquerda ({{x_1}, {x_4}, {x_3}, {x_4}} dereita) \) tal que:
\
Atopamos as ecuacións que definen \ (^ \ BOT} \):
\
Buscar unha base de \ (^ \ BOT } \):
\
DIG = “15FAA2E3F9”>
\
Propiedades do complemento Ortogonal
mar \ (V) un espazo de vectores de dimensión de dimensión, con produto interno e ser \ (s) un subespacio de \ (V \). A continuación, as seguintes propiedades son verificados:
- \ ({\ left ({^ \ bot}} \ right) ^ \ bot} = s \)
- \ ({V ^ \ BOT} = \ ({V ^ \ BOT} = \ ({{{\; {0_V} \;} \ right \} \) e \ (\ esquerda {{\; {0 {V \;} }} \ Right \} {\; \ BOT} = v \)
- \ (s ^ ^ ^ \ BOT} = \ esquerda \ {{{0_v}} \ rightsht \) \)
- \ (S + {S ^ \ BOT} = V \)
Esta última propiedade significa que calquera vector \ (V) pode expresarse como unha suma dun Vector de máis que \ ({S ^ \ BOT} \).
Ilustrar cun exemplo xeométrico de \ ({\ mathbb {R} ^ 3} \):
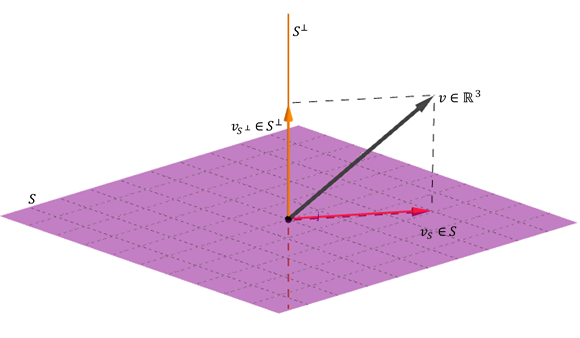
de propiedades 3 e 4 é deducido:
e, polo tanto:
A unión dunha base \ (s \) cunha base de \ ({^ \ BOT} \) é a base de \ (V). Isto aplícase para ampliar unha base de \ (\; \) a unha base de \ (V \), como se mostra como o seguinte exemplo.
exemplo
mar \ (s = \ esquerda \ {{\ esquerda ({{x_1}, {x_2}, {x_3}, {x_4}} dereita) \ en {\ mathbb {R} ^ 4} \;: \; \; {x_1} + {x_4} = 0; \; \; \; {x_1} – {x_2} + 3 {x_4} = 0 \;} \ right \} \).
Atopar unha base de \ ( S \) e estendelo a unha base de \ ({\ mathbb {R} ^ 4} \).
resolución
Estamos a buscar un s, por exemplo:
\
como \ (dim \ (s \ r dereita) = 2 \), podemos anticipar iso: \ (Dim ({s) ^ \ BOT} \)) = 4-2 = 2
da base de s, obtemos as ecuacións de \ (^ \ BOT} \):
\
e atopamos unha base de \ (^ \ BOT} \), por exemplo:
\
A continuación, unirse ás bases de \ (s \) e \ ({^ \ BOT} \) resultados:
\ (b = \ esquerda {{\ esquerda ({1, – 2.0, – 1} →), \ esquerda ({0,0,1,0} \ right), \ esquerda ({2,1.0.0) \ right), \ esquerda ({0.1.0, – 2} dereita) )} \ dereito \} \) base de \ ({\ mathbb {R} ^ 4} \)
Exercicio para o lector 7
Dado os seguintes subprodacios \ ({\ mathbb {R} ^ 4} \):
\ (S = \ á esquerda {{\ esquerda ({{x_1}, {x_2}, {x_3}, {x_4}} dereita) \;: \; \; {x_1} = 0 \; \; \; \; \; {x_2} + 2 {x_3} = 0 \;} \ right \} \) e \ (w = xene \ esquerda {{\ \; \ esquerda ({1,0.0.0) \ right), \ esquerda ({{ 2,3, k, 0} \ right)} \ right \} \)
Atopar os valores de \ (k \) para os que \ (w = \; {s ^ \ BOT} \).