Demostración de fórmulas de área e volume usando integrais

bo! Nesta entrada as fórmulas que todos coñecemos sobre a área e volume de corpos coñecidos como cubos, círculos, esferas, pirámides …

Para iso demostraranse, por suposto, utilizaremos a integración numérica, Unha ferramenta matemática esencial para calquera tipo de cálculo que inclúa unha suma infinitesimal de valores diferentes.

para poder comprender perfectamente determinados cálculos expostos que ten que saber Polo menos se integra nunha variable, e é moi recomendable visitar este artigo: integrales dobres e triples. Cambios de variables

Táboa de contidos

as fórmulas

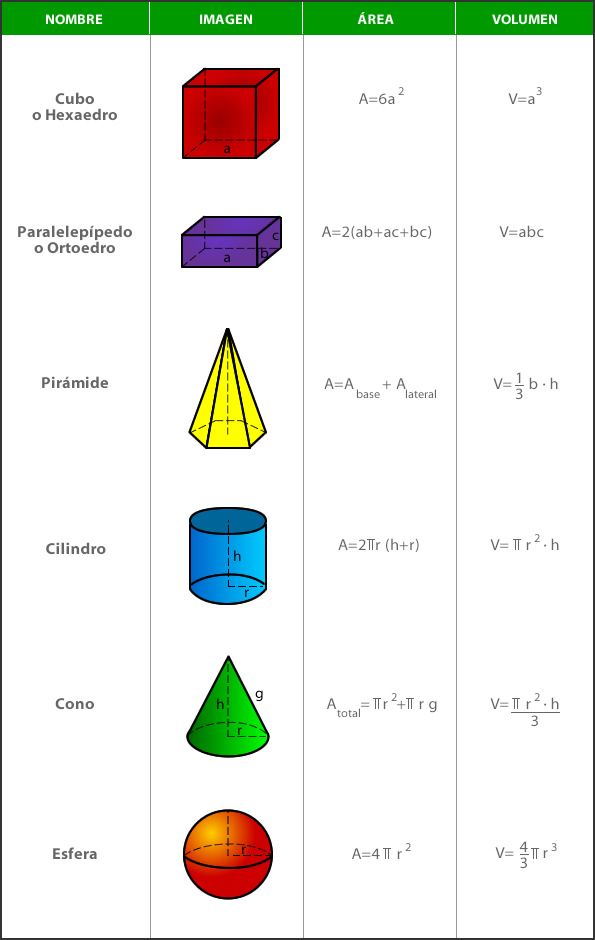
para calcular unha área ou volume, o que se fai é calcular a integral (simple, dobre, triple, curvilinear, superficie …) da función constante f = 1 no recinto cuxas dimensións Queremos calcular.

Paralelepípedo

Empregando integrais para este corpo xeométrico equivale a matar moscas a Cannon; Non obstante, como a primeira utilidade básica de integrais dobres e triples calcularemos o seu volume

volume

O noso recinto de integración é un paralelepípedo de lados A, B e C. Polo tanto, a integral permanece:

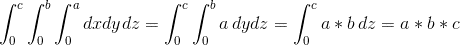
círculo

Todo o mundo sabe as súas fórmulas:

$2 \ pi r$ e $\ pI r 2$ . Pero, como se deducen?

Primeiro de todo, debemos saber que se queremos representar gráficamente unha función de circunferencia, non pode ser representado de forma tan fácil a partir da forma e = f (x) xa que non é inxectada, Dito, por un valor X, aparecen 2 valores e (a fórmula xeral para un RY RY centrada na orixe de coordenada é

<2} = r 2

. (No caso de querer pintar un círculo, só cambia = por < =). Polo tanto, úsase a parametrización:

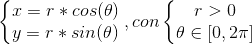
Demostración de fórmulas de área e volume a través de integrais 2

cuxa determinación de jacobiano, para o cambio de variables é: r

Se queres saber máis sobre a circunferencia e como obtén a túa fórmula dun xeito máis detallado, este é o teu artigo

Aquí podes xogar un pouco co Ecuación da circunferencia: ligazón ao desmos

perímetro

o r ECCTO é que “fío” que compón o bordo exterior do círculo. Polo tanto, a curva parametrizada do devandito fío é:

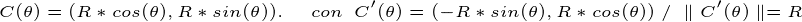
Demostración de fórmulas de área e volume por integrales 3

calcular a integral curvilinear na función constante F = 1 — >

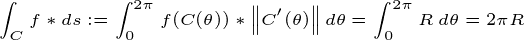
área

para calcular A área, basta con calcular a integral no recinto delimitado pola circunferencia. Para facilitar os cálculos que pasamos de coordenadas cartesianas (x, y) a polares (r,

$\ theta$ ) usando o jacobiano R para o cambio de variable. $\ int_ {s} dxdy = \ int_ {0} ^ {} \ int_ {0} ^ {2 \ pi} r drd \ theta = 2 * \ pi \ int {0} ry r dr = 2 * \ pi * \ frac {r 2} {2} = \ pi * r 2$

Sphere

O caso da esfera que as súas fórmulas son un pouco máis descoñecidas.

$\ frac {4} {3} * \ pi * r 3$ para volume e para a área da súa superficie.

Como co círculo, usaremos outras coordenadas, as coordenadas esféricas. A ecuación da esfera en cartesianas é

A parametrización en:

$\ esquerda \ {\ begin {matrix} x = r * sen (\ theta) * cos (\ phi) \\ y = r * sen (\ theta) * sen (\ phi) \\ z = R * cos (\ theta) \ end {matrix} \ right$ , con $\ esquerda \ {\ begin {matrix} 0 \ leq r \ leq r \\ 0 leq \ Phi \ leq 2 \ leq \ pi \ end {matrix} \ right$

cuxo jacobiano é

$r 2 * sen (\ theta)$

Aquí podes xogar un pouco coa ecuación da esfera: Introduza GeoGebra 3D e pegue isto no editor: Superficie (R * SEN (U) * COS (V), R * SEN (U) * SEN (V) , R * cos (u), u, 0, pi, v, 0,2pi)

área

Para calcular a área, basta con calcular o intervalo de viaxes por A parametrización con R = R.Calculamos a integral facendo o cambio de variable co jacobiano.

$\ int \ int_ {s} dxdy = \ int_ {0} ^ {\ pi} \ int_ {0} ^ {2 \ pi} r 2 * sen (\ theta) d \ d \ phi = 2 * \ pi * r 2 * \ int_ {0} ^ {\ pi} sen (\ theta) d \ theta = 4 * \ PI * R 2$

Volume

Para o volume que calculamos a integral do recinto enteiro

usando as variables $DRD \ theta d \ phi$ $\ int / int_ {v} dxdydz = \ int_ {0} ^ {\ pi} \ int {0} \ {r} \ int_ {0} ^ {2 \ pi} r 2 * sen (\ theta) d \ theta d \ phi = 2 * \ pi * \ int {0} ^ {\ pi} \ int {0} ° r 2 * sen (\ theta) d \ theta Dr \ rightarrow$ $\ rightarrow 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ° R 2 * sen (\ theta) d \ theta dr = \ frac {2} {3} * \ pi * r 3 \ int_ {0} ^ {\ pi} sen (\ theta) d \ theta = \ frac {4 } {3} * \ pi * r 3$

pirámide

A forma de calcular o volume dunha pirámide é idéntica á dun paralelepipado; A complicación é establecer os límites de integración (o recinto).

Tirando a lóxica, a coordenada Z será gratuíta, variando de 0 a h. As coordenadas de Xey dependerán da coordenada Z sobre os valores máximos que levan, a partir de -b / 2 AB / 2 como máximo na base e tomando como un único valor 0 cando o Z = H (Pyramid Peak). Baseado neste enfoque, tomamos os límites das variables:

$\ esquerda {\ begin {matrix} - \ frac {B} {2} * (1- frac {z } {H) \ leq x ≤ \ frac {B} {2} * (1- frac {z} {h) \\ - \ frac {B} {2} * (1- frac {z} {h ) \ leq e \ leq \ frac {B} {2} * (1- \ frac {z} {h) \\ \ leq z \ leq h \ end {matrix} \ right$

volume

Calculamos a integral no recinto DXDYDZ

$v = \ iiint_ {v} dxdydz = \ int_ {0} ^} \ int_ {- \ frac {b } {2} * (1- frac {z} {h)} ^ \ frac {B} {2} * (1- \ frac {z} {h)} \ int {- \ frac {B} {2 } * (1- \ frac {z} {h)} ^ \ frac {B} {2} * (1- frac {z} {h)} d e dx = \ int_ {0} {h} b 2 * (1- \ frac {z} {h) 2 dz = \ rightarrow$

cone

O cono é moi similar á pirámide. Non obstante, debemos usar coordenadas polares para parametrizar correctamente a base circular. Usaremos as variables

$\ z, \ r \ y \ \ theta$ . Seguindo unha dedución similar á pirámide que nos deixamos: $\ esquerda \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 leq r \ leq r * (1- frac {z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ end {matrix} \ right$

volume

Calculamos a integral no recinto Dixydz e Facemos o cambio de variable a polar con jacobiano r

$v = \ iiint_ {v} dxdydz = \ int_ {0} ^ \ int_ {0} q (1- frac { Z} {h)} \ int_ {0} ^ {2 \ pi} r \ dzdrd \ theta = \ pI \ int {0} ^ {h} r$ * (1- crac {z} {h) 2 = \ rightarrow

$= \ rightarrow \ pi * r 2 \ int {0} ^ ^ {h} (1+ \ frac {z 2} {h 2} - \ frac {2z} {h) = \ pi * r 2 * 0 ^ {h} = \ pi * r 2 * \ frac {h} {3}$

que, como anticipamos, como a pirámide a súa fórmula é

$área \ de \ a base * \ frac {altura} {3}$

cilindro

O cilindro é quizais a figura máis intuitiva ao calcular a área da superficie eo seu volume. A pesar de ser obvio, mostraremos como o seu volume pode ser calculado de forma integral (ser, claramente, área base * altura) para que a operación de triple integrais sexa mellor entendida.

usaremos As variables

$\ z, \ r \ y \ \ \ theta$ tal: $\ esquerda \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq r \\ \ pi \ end {matrix} \ right$

volume

Calculamos a integral sobre o recinto DXDYDZ e facer o cambio de variable a polar con jacobiano r

$v = \ iiint_ {v dxdydz = \ int_ {0} ^ {h} \ int {0} ^ {r} \ int_ {0} 2 r \ dzdrd \ theta = 2 \ pi \ int {0} ^ {h} \ int {0} ° r \ dzdr = \ rightarrow$ $\ rightarrow = \ Pi * r 2 * \ int_ {0} ^ h dz = \ pi * r 2 * h$

as fórmulas

Paralelepípedo

volume

círculo

perímetro

área

Sphere

área

Volume

pirámide

volume

cone

volume

cilindro

volume

Deixa unha resposta Cancelar a resposta