démonstration de formules de surface et de volume via des intégrales

Posted on décembre 10, 2020 by admin

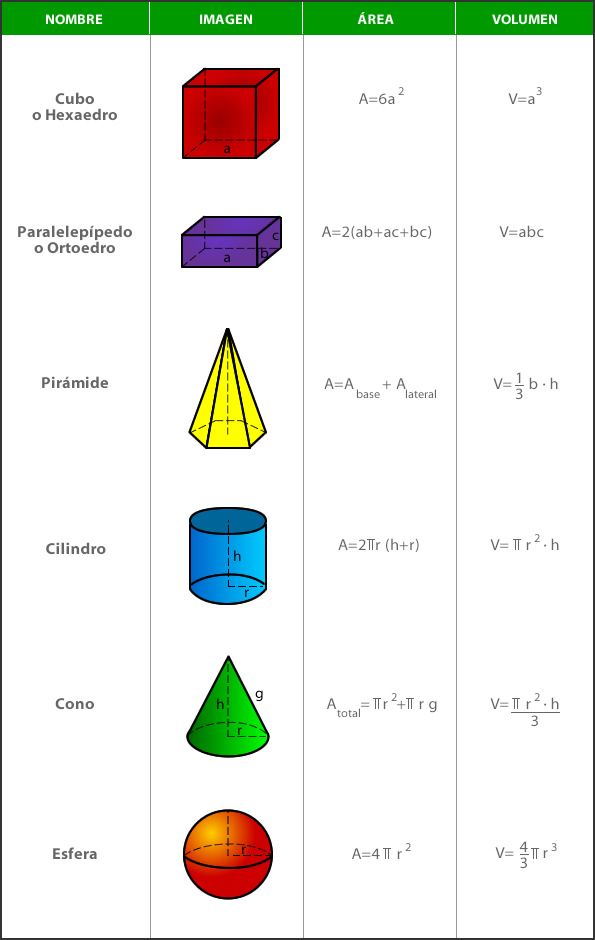
bien! Dans cette entrée, les formules que nous connaissons tous sur la zone et le volume de corps appelés cubes, cercles, sphères, pyramides …

car cela sera démontré, bien sûr, nous utiliserons l’intégration numérique, un outil mathématique essentiel pour tout type de calcul comprenant une somme infinitésimale de valeurs différentes.

Pour pouvoir comprendre parfaitement certains calculs exposés que vous devez savoir Au moins intégrer dans une variable et il est fortement recommandé de visiter cet article: double et triple intégral. Modifications de variables

Table des matières

Les formules

Pour calculer une zone ou un volume, ce qui est fait est de calculer l’intégrale (simple, double, triple, curvilinéaire, surface …) de la fonction constante F = 1 sur le boîtier dont les dimensions dont les dimensions Nous voulons calculer.

parallélépípedo

Utiliser des intégrales pour ce corps géométrique équivaut à tuer des mouches au canon; Cependant, en tant que première utilité de base des intégrales doubles et triples, nous calculerons son volume

volume

Notre boîtier d’intégration est un parallélépipède des côtés A, B et C. Par conséquent, les restes intégrale:

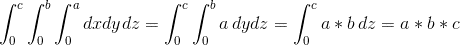
cercle

Tout le monde connaît ses formules:

$2 \ pi r$ et $\ pi R 2$ . Mais, comment déduisent-ils?

Tout d’abord, nous devons savoir que si nous voulons représenter graphiquement une fonction de circonférence, elle ne peut pas être aussi facilement représentée de la forme et = f (x) car il n’est pas injectif, Il dit que pour une valeur x, 2 valeurs apparaissent et (la formule générale d’un rayon ry centré sur l’origine de la coordonnée est

<2} = r 2

. (Dans le cas de vouloir peindre un cercle, il suffit de changer = par < =). Par conséquent, le paramétrage est utilisé:

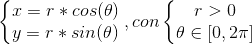
Démonstration de formules de surface et volume via des intégrales 2

dont la détermination de Jacobiano, pour le changement de variables est: r

Si vous voulez en savoir plus sur la circonférence et comment vous obtenez votre formule de manière plus détaillée, ceci est votre article

ici, vous pouvez jouer un peu avec le Équation de la circonférence: Lien vers Desmos

Perimeter

le r ECCTO est ce « fil » qui constitue le bord extérieur du cercle. Par conséquent, la courbe paramétrée dudit fil est la suivante:

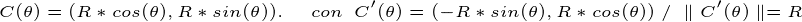
Calcul de l’intégrale curviligne sur la fonction constante F = 1 — >

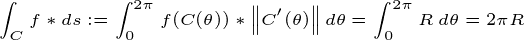
Démonstration de formules de surface et de volume par intégrales 4

zone

pour calculer La zone, il suffit de calculer l’intégrale sur le boîtier délimité par la circonférence. Pour faciliter les calculs que nous passons de coordonnées cartésiennes (x, y) à polares (r,

$\ theta$ ) en utilisant le jacobiano r pour le changement de variable. $\ int_ {s} dxdy = \ int_ {0} ^ {} \ int_ {0} ^ {2 \ pi} r drd \ theta = 2 * \ pi \ int_ {0} ry r dr = 2 * \ pi * \ frac {r 2} {2} = \ pi * r 2$

Sphère

Le cas de la sphère Ses formules sont un peu plus inconnues.

$\ frac {4} {3} * \ pi * r 3$ pour le volume et $4 * \ pi * r 2$ Pour la zone de sa surface.

Comme avec le cercle, nous utiliserons d’autres coordonnées, les coordonnées sphériques. L’équation de la sphère dans les cartésianas est

Le paramétrage en:

$\ Gauche \ {\ commencez {matrice} x = r * sen (\ theta) * cos (\ phi) \\ y = r * sen (\ theta) * sen (\ phi) \\ z = R * cos (\ theta) \ fin {matrice} \ droite$ , avec $\ gauche \ {\ commencements {matrice} 0 \ Leq r \ leq r \\ 0 \ Leq \ Phi \ Leq 2 \ LEQ \ PI \ End {matrice} \ droite$

Quel jacobien est

$R 2 * SEN (\ theta)$

Ici, vous pouvez jouer un peu avec l’équation de la sphère: Entrez Geogebra 3D et coller ceci dans l’éditeur: Surface (R * Sen (U) * COS (V), R * SEN (U) * SEN (V) , R * cos (u), u, 0, pi, v, 0,2pi)

zone

Pour calculer la zone, il suffit de calculer la gamme de voyages par Le paramétrage avec R = R.Nous calculons l’intégrale en faisant le changement de variable avec le jacobien.

volume

pour le volume Nous calculons l’intégrale de l’ensemble de l’enceinte

à l’aide des variables $DRD \ theta d \ phi$ $\ int / int_ {v} dxdydz = \ int_ {0} ^ {\ pi} \ int_ {0} \ {r} \ int_ {0} ^ {2 \ pi} R 2 * SEN (\ theta) d \ theta d \ phi = 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ° R 2 * Sen (\ theta) d \ theta dr \ RightArrow$ $\ RightArrow 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ° R 2 * SEN (\ theta) d \ theta dr = \ frac {2} {3} * \ pi * r 3 \ int_ {0} ^ {\ pi} Sen (\ theta) d \ theta = \ frac {4 } {3} * \ pi * r 3$

pyramide

Le moyen de calculer le volume d’une pyramide est identique à celui d’un parallélépipède; La complication consiste à établir les limites d’intégration (l’enceinte).

Logique de tirage, la coordonnée Z sera libre, variant de 0 à h. Les coordonnées Xey dépendront de la coordonnée Z concernant les valeurs maximales qu’ils prennent, à partir de -b / 2 AB / 2 au plus à la base et prenant comme une valeur unique 0 lorsque le z = h (pyramid pic). Sur la base de cette approche, nous prenons les limites des variables:

$\ gauche {\ commencent {matrix} - \ frac {b} {2} * (1- \ frac {z } {H) \ Leq x ≤ \ frac {b} {2} * (1- \ frac {z} {h) \\ - \ frac {b} {2} * (1- \ frac {z} {h ) \ Leq et \ leq \ frac {b} {2} * (1- \ frac {z} {h) \\ \ lq z \ fin \ fin {matrix} \ droite$

volume

Nous calculons l’intégrale sur le boîtier DXDYDZ

$v = \ iiint_ {v} dxdydz = \ int_ {0} ^} \ int_ {- \ frac {b } {2} * (1- \ frac {z} {h)} ^ \ frac {b} {2} * (1- \ frac {z} {h)} \ int_ {- \ frac {b} {2 } * (1- \ frac {z} {h)} ^ \ frac {b} {2} * (1- \ frac {z} {h)} d et dx = \ int_ {0} ^ {h} b 2 * (1- \ frac {z} {h) 2 dz = \ RightARrow$

cône

Le cône est très similaire à la pyramide. Cependant, nous devons utiliser des coordonnées polaires pour paramétrer correctement la base circulaire. Nous utiliserons les variables

$\ z, \ r \ y \ theta$ . Après une déduction similaire à la pyramide, nous avons quitté: $\ GAUCHE \ {\ BEGN {matrice} 0 \ Leq z \ LEQ H \\ 0 \ LEQ R \ LEQ R * (1- \ frac {z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ fin {matrice} \ droite$

volume

Nous calculons l’intégrale sur le boîtier de DixyDz et Nous faisons le changement de variable à polaire avec jacobiano r

$v = \ iint_ {v} dxdydz = \ int_ {0} ^ \ int_ {0} q (1- \ frac { Z} {h)} \ int_ {0} ^ {2 \ pi} r \ dzdrd \ theta = \ pi \ int_ {0} ^ {h} r$ * (1- \ crac {z} {h) 2 = \ RightARrow

$= \ Right Drive \ pi * r 2 \ int_ {0} ^ ^ {h} (1+ \ frac {z 2} {h 2} - \ frac {2Z} {h) = \ pi * r 2 * 0 ^ {h} = \ pi * r ^ {2} * = \ pi * r 2 * \ frac {h} {3}$

Ce que, comme nous l’avons prévu, tout comme la pyramide, sa formule est

$zone \ de \ la base * \ frac {hauteur} {3}$

Cylindre

Le cylindre est peut-être la figure la plus intuitive lors du calcul de la zone de la surface et de son volume. En dépit d’être évident, nous montrerons comment votre volume pourrait être calculé de manière intégrale (étant clairement de la hauteur de la zone de base) afin que le fonctionnement des triple intégrales soit mieux compris.

Nous utiliserons Les variables

$\ z, \ r \ \ \ \ theta$ telle: $\ GAUCHE \ {\ commencez {matrice} 0 \ LEQ Z \ LEQ H \\ 0 \ LEQ R \ LEQ R \\ \ PI \ Fin {matrice} \ droite$

Volume

Nous calculons l’intégrale sur le boîtier DXDYDZ et faire le changement de variable à polaire avec jacobiano r

$v = \ iint_ {v dxdydz = \ int_ {0} ^ {h} \ int_ {0} ^ {r} \ int_ {0} 2 r \ dzdrd \ theta = 2 \ pi \ int_ {0} ^ {h} \ int_ {0} ° r \ dzdr = \ rightarrow$ $\ RightARrow = \ Pi * R 2 * \ int_ {0} ^ h dz = \ pi * r 2 * h$

Les formules

parallélépípedo

volume

cercle

Perimeter

zone

Sphère

zone

volume

pyramide

volume

cône

volume

Cylindre

Volume

Laisser un commentaire Annuler la réponse