… ou comment la chance est de votre côté pour obtenir plus de note
Vous faites un Test de type test, il y a quatre questions que vous ne savez pas comment répondre et réagir à tort, vous soustrayez vos points. Si vous décidez de répondre aux quatre questions au hasard, il est très susceptible de terminer plus de points que si vous n’y répondez pas. Cette affirmation semble correcte, en tenant compte du fait que s’il ya quatre questions avec quatre options de réponse, il est logique de supposer qu’il est le plus susceptible d’échouer trois fois et d’en frapper un, si nous supposons que vous frappez un point et que vous échouez, Dans le cas plus probablement, nous serons les mêmes. Vaut-il une rose? Est-ce que la même chose se passe avec un nombre différent de réponses aléatoires? Il s’avère que les mathématiques ont quelque chose à dire à ce sujet …
Les examens de type de test présentent une série de réponses à partir desquelles vous devez choisir, normalement une réponse correcte. Dans certains tests de type de test, il y a plus d’une réponse correcte, parfois les défauts soustrayez des points, il peut y avoir des réponses pondérées ou une limite de questions pouvant être échouées.
<
Puis-je approuver si je fais un test de type de test sans étude?
L’idée de cet article est de répondre aux questions de style: puis-je approuver si je fais un test de type test sans étudier? Est la probabilité de mon côté si j’ai répondu au hasard? Est-ce que la même chose se produit dans n’importe quel type de test? Quelle est la différence si les défauts soustraient ou non? Quelle probabilité dois-je approuver si je réponds à moitié aléatoire? Et si je suis sûr la moitié? Et pour obtenir un remarquable? Et un exceptionnel? …
Nous avons commencé dans l’examen de type de test le plus simple, les succès ajoutés, les échecs et les réponses sans réponse n’ont aucune incidence sur la note.
Calcul de la note. ..
Nous définissons des noms de variables:
n = nombre total de questions
A = nombre de succès
n = note finale
Si nous supposons que la note est un nombre de 0 à 10 et l’examen dispose de 10 questions que le calcul de la note est trivial . La note obtenue est égale au nombre de questions réussies:
= « 1185f5E344″>
… avec une baremo
Si l’examen comporte un certain nombre de questions autres que la Barte de la note, pour obtenir la note finale, vous devez diviser le nombre de succès entre le nombre de questions et multiplier par limite de bordure supérieure.
pour Exemple: si la baremo est de 0 à 10 et il y a 40 questions à l’examen, pour sortir un 5, vous devez atteindre 20 questions. C’est-à-dire que le nombre de questions réussies entre le nombre total: 20/40 = 0,5 et multiplier le résultat par la limite supérieure de la barème: 0,5 × 10 = 5.
généralisant, pour calculer une note dans un type Test d’examen dans lequel les défaillances ne sont pas soustraits et nous avons une BARTE:
Bₛ = Limite d’alésage supérieur
« >
Calculement des probabilités …
est assez évident que peu importe Que vous sachiez ou non les réponses, si les échecs ne soustraient pas les points, la meilleure option est de répondre à tout. Disons qu’en matière de points, vous n’avez pas littéralement rien à perdre.
Dans tous les cas, formulons de former la question avec des mathématiques, combien de combinaisons de réponses sont possibles? Et comment dépend de ce nombre?
… avec une question
Le cas trivial est avec une seule question. Si nous avons 4 options de réponse: A, B, C, D. Il y a 4 possibilités:
La probabilité qu’un événement se produise est le nombre d’événements possibles Parmi les fois où l’événement se produit en question. Dans ce cas, il existe 4 événements possibles, seulement 1 implique de frapper et de défaillance:
La probabilité de frapper la réponse à une question aléatoire est d’une question entre quatre: 1/4 = 0,25. Normalement, nous disons une chance de 25% de frapper.
La probabilité d’échec serait trois entre quatre: 3/4 = 0,75. C’est-à-dire que c’est 75%.
Comme on voit, dans ce cas une réponse aléatoire a tout à perdre. Il est également intéressant de noter que si nous ajoutons les deux cotes, nous obtenons 100% depuis, dans ce cas, il n’y a que deux résultats possibles: frapper ou échouer. Nous verrons que ce n’est pas le cas s’il y a plus d’une question.
en résumé …
… avec deux questions (ou plus)
avec deux questions que nous pouvons répondre par exemple: dans le premier déjà dans le second, dans la première et b du deuxième, b dans la première déjà dans la seconde … Ce sont toutes les combinaisons possibles:

Ce sont, en bref Tous les événements possibles répondent à deux questions. Ils ont 16 ans. Quatre fois plus de possibilités qu’avec une question. Ce 4 vient du fait que nous avons 4 options de réponse, et ce qui se passe est que chaque fois que nous ajoutons une question, nous multiplions par 4 les combinaisons possibles des réponses:
P₁ = nombre d’options de la question 1
P₂ = nombre d’options de la question 2
C₂ = nombre de combinaisons de deux réponses
La formule serait la suivante:
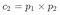
Dans ce cas:

en général, il vous suffit de multiplier par le nombre d’options, autant de fois que des questions il y a :

Cette formule est facile à simplifier, considérant que le nombre d’options est toujours le même: P₁ = P₂ = P₃ = … = pₙ. Si nous définissons:
n = nombre de questions
P = nombre d’options dans chaque question
Le nombre de combinaisons est calculé comme suit:
dans ce cas, avec p = 4 et n = 2:
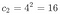
L’étape suivante est pour calculer les chances. Dans ce cas, il existe trois événements possibles:
- succès toutes les questions.
- Atteint une question (et échouez l’autre).
- échoue . questions
la prise en compte de tous les événements possibles, il n’y a qu’un seul cas où toutes les questions sont acceptées, en supposant que les deux réponses sont A:

Par conséquent , la probabilité de toucher les deux questions est 1/16 = 6.25%.
Généralisation , la probabilité d’obtenir tout donné un certain nombre de questions N est 1 entre toutes les combinaisons possibles de réponses, qui est:


une probabilité de 4,25% est déjà assez faible, mais voyons comment ce pourcentage diminue considérablement en fonction de Nous augmentons le nombre de questions que nous répondons au hasard. Par exemple, avec 10 questions:
>
Comme on le voit, il y a plus d’un million les combinaisons possibles, par conséquent, la probabilité de toucher toutes les réponses aléatoires est minuscule.
… En fait, il est beaucoup plus susceptible de toucher à la loterie.
Mais nous ne sommes pas aussi ambitieux, vous n’avez pas besoin de frapper tout. Quelle probabilité existe-t-il d’en obtenir? En supposant à nouveau que les bonnes réponses sont les A, ce sont les moments que nous avons touché une réponse à deux questions:

Notez que nous n’avons pas souligné AA car ils sont deux succès, pas un.
Nous avons 6 combinaisons possibles qui nous donnent une réponse réussie, la probabilité est de notre côté:

La probabilité d’augmenter quelque chose serait la somme des deux précédents, ou quel est le même, ajouter la possibilité d’obtenir tout les possibilités de toucher un:


est pas mal, d’avoir répondu à tout au hasard.
la seule chose qui reste est de connaître la probabilité de tout échouer, et puisque c’est le seul ou événement que notre probabilité reste constituera ce qui est prêt à atteindre 100%, ou quel est le même, le reste des combinaisons possibles si nous soustrayons le succès:
Ainsi , la probabilité de ne dépasse cinquante pour cent, donc nous pouvons parier que nous allons sûrement pas ajouter des points répondre à deux questions aléatoires.
Donc, la table sommaire aurait-elle ajouté les chances avec deux questions: