la visió és el sentit mitjançant el qual obtenim la major informació sobre el nostre entorn . La interpretació que fa el nostre cervell, basat en la informació que rep dels ulls, està fortament influenciada per l’experiència; això a vegades comporta a cometre errors d’apreciació. Al llarg de el temps de la seva vida, i sobretot en les edats més primerenques, un individu categoritza, generalitza i caracteritza els elements del seu entorn per poder prendre decisions ràpidament. Persones que tenen deficiències en el seu sentit de la vista poden corregir o reduir els defectes d’aquesta per mitjà de lents, això és possible si parlem de problemes d’enfocament per exemple. Amb el desenvolupament en l’adquisició d’imatges a través d’eines tecnològiques també ha sorgit la necessitat de corregir aquestes imatges perquè la seva posterior interpretació sigui verídica. Si un dispositiu d’adquisició d’imatges lliurament imatges amb defectes d’enfocament, es pot corregir aquesta deficiència afegint lents a el dispositiu. La perspectiva és un aspecte important a l’hora d’interpretar una imatge, el fonament d’aquest aspecte està en l’experiència, ja que així és com aprenem a estimar mesures, posicions, velocitats, etc. Es pot aconseguir una interpretació precisa de la imatge obtinguda si les característiques de l’objecte allà continguts són conegudes per l’individu que l’analitza. Allà es troba la importància que les proporcions de la imatge, pel que fa a la realitat, siguin congruents. També fem ús de la perspectiva per suggerir una idea a un individu o persuadir-lo, i allí trobem valor a l’hora de modificar les proporcions dels elements en una imatge. Quan la imatge adquirida no correspon al que volem visualitzar podem fer una modificació de la imatge perquè sigui més convenient.
Per modificar una imatge s’usen transformacions de coordenades dels píxels i modificacions en la brillantor de la imatge, això últim s’aconsegueix amb tècniques d’interpolació de la brillantor. Canviar les proporcions de la imatge es pot comprendre amb una acció anàloga: si tenim una superfície de gel i expandim aquesta superfície amb calor obtindrem una superfície de vapor i existiran regions buides en aquesta superfície. El mateix efecte succeeix a les imatges i per compensar aquest defecte es fan servir tècniques d’interpolació; amb aquestes tècniques li assignem valors als llocs buits perquè la imatge s’apreciï uniforme, això està relacionat amb la resolució dela imatge. La manera en què afectem la geometria de la imatge es basa en tècniques de transformacions geomètriques. Si volem desplaçar la imatge, canviar les seves proporcions de base i alçada, girar o lliscar podem realitzar la transformació lineal afí. Si es vol canviar la geometria de la imatge sense conservar el paral·lelisme entre les rectes oposades de el contorn de la imatge podem usar una transformació Bilineal o una transformació Perspectiva. Aquesta transformació fa servir 4 punts de referència i 4 punts de transformació per a definir la funció de transformació.


EL objectiu d’aquesta pràctica és modificar una imatge d’altura “i” i base “x”. la imatge serà modificada a partir de dos punts de la imatge. per formular el problema i descriure la solució proposada es farà ús d’una imatge d’exemple. es vol modificar la imatge 2, per això es selecciona el píxel marcat amb una “X” vermella i es marca la posició a la qual es vol portar amb una “O” roj a, per a aquest cas. El punt de referència “X” tindrà les coordenades (prx (1), PRY (1)). El punt de referència “O” tindrà les coordenades (prx (2), PRY (2)). El primer element de l’anterior nomenclatura correspon a la posició en l’eix horitzontal i el segon element correspon a la posició en l’eix vertical. S’ha de tenir en compte que per ubicar aquests punts el punt origen de referència està a la cantonada superior esquerra de la imatge.
Es farà servir la transformació lineal per modificar una imatge basat en la selecció de dos píxels de la imatge. Primer es selecciona el píxel “1” i posteriorment el píxel “2”.La imatge canviarà pel que fa a aquests dos punts de referència; es desitja moure el píxel “1” a la posició de l’píxel “2”, tota la imatge ha de canviar per acomodar-se a aquest nou punt de referència. Dividint la imatge en 16 cel·les iguals (4×4), la solució és que cada cel·la canviï a una forma específica i totes aquestes noves manera es puguin unir per aconseguir una nova imatge de les mateixes dimensions de l’original. L’anterior es pot aconseguir fent ús de la transformació bilineal aplicada a cada cel·la.
La solució proposada està pensada per a imatges conformades per una sola matriu, de manera que no es pot aplicar aquesta transformació a imatges en format RGB per exemple.
Desenvolupament de l’exercici.
a la imatge 2 aquesta superposada una malla de color blau, la qual haurà de canviar pel que fa a la transformació desitjada. Aquesta malla té 3 línies verticals i 3 línies horitzontals. La solució a el problema original és una solució general, així que només es fa servir la imatge d’exemple en certs moments de la descripció perquè sigui més clara l’explicació.
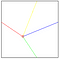
El primer que es fa és ubicar línies de referència a dalt, a baix, a la dreta ia l’esquerra del punt “X”. Són les línies més curtes des del punt “X” cap als extrems de la imatge, com s’observa en la imatge 3.A. Les coordenades del punt “X” són (prx (1), PRY (1)).
Després de situar les línies de referència es troben els punts de tall de cada línia de la malla amb aquestes línies de referència. És possible que les línies de referència tinguin punts de tall amb tres, amb dos, amb una o cap línia de la malla. a continuació es mostren els punts d’intersecció per a aquest cas en la imatge 4.

Es tracen quatre línies de referència noves per graficar la nova malla. el punt on s’uneixen aquesta 4 noves línies és el punt “O” les coordenades són (prx (2), PRY (2)). d’aquesta manera la línia groga part de el punt (prx (2), PRY (2)) fins al punt (prx (1), 1) l’1 correspon a la primera fila de píxels de la imatge, la línia blava part de l’pu nt (prx (2), PRY (2)) fins al punt (x, PRY (1)) la x correspon a la ultima columna de píxels de la imatge, la línia vermella part de el punt (prx (2), PRY ( 2)) fins al punt (1, PRY (1)) l’1 correspon a la primera columna de píxels de la imatge i la línia verda part de el punt (prx (2), PRY (2)) fins al punt (prx ( 1), i) la columna i correspon a la ultima fila de píxels de la imatge, com es mostra a la imatge 5.
Si ens fixem, la ubicació dels punts d’intersecció, en la il·lustració 3, hauran de canviar en proporció a el canvi de la línia sobre la qual estan ubicats. Després de trobar la proporció amb què canvien i situant-los en la seva nova posició obtenim el següent resultat: imatge 6.

En la vora de la imatge 6 s’assenyalen els punts d’on parteixen les línies que conformen la malla, a partir d’aquests indicadors i els nous punts d’intersecció es traça la nova malla. A la imatge 7 es pot apreciar això.

els valors que ens importen a la imatge 7 són aquells que indiquen els punts d’intersecció de les rectes discontínues.

Unint aquests punts d’intersecció es pot graficar la nova malla. La nova malla s’usa per referència visual, ja que per realitzar la transformació Bilineal només necessitem els punts d’intersecció.

La identificació de la intersecció dels punts es realitza amb equacions de recta, simplement es calcula la cruïlla dels línies que generen els punts d’interès.
Ara que es coneixen els nous punts de la malla podem realitzar la transformació Bilineal de cada cel·la. Realitzant la transformació per a la cel·la on es troba la major part de la cara de Lena es pot explicar el procés de transformació.

Es realitza la transformació en una regió rectangular que contingui a la nova regió, és a dir, una regió rectangular on aquest continguda la regió delimitada per k5, k8, K9 i k6. Prenent com a entrada els punts que emmarquen cada cel i els nous punts realitzem la transformació Bilineal. Després de la transformació obtenim la imatge 11 per a la cel·la.

Si fem la transformada a totes les cel · les i superposem les regions obtingudes el resultat de la imatge 12.

Per evitar la superposició de les regions, com veiem en la imatge 12, hem de retallar les regions abans de superposar entre si. Si tallem la cel·la de la imatge 11 amb el contorn k5, k8, K9 i k6 de la imatge 9 obtenim el resultat de la imatge 13.

Després de realitzar les retallades i superposar les regions retallades s’obté el resultat de la imatge 14.

Vaig permetre que les vores de les regions es superposen per observar com s’afecta la malla.
Resultat de diferents punts.

Codi MATLAB
Amb el següent codi podràs posar en pràctica pas a pas la transformació. Segur podràs optimitzar-lo.
clc; clear all; close all;im=imread(‘LenaMonoColor.bmp’);
=size(im);
a=round(x/4); %horizontal
b=round(y/4); %vertical
figure;imshow(im);
% =ginput(2);
% hold on;for k=0:5;
line(,);
line(,);
endim1=uint8(zeros(size(im)));
im2=uint8(zeros(size(im)));
im3=uint8(zeros(size(im)));
im4=uint8(zeros(size(im)));
im5=uint8(zeros(size(im)));
im6=uint8(zeros(size(im)));
im7=uint8(zeros(size(im)));
im8=uint8(zeros(size(im)));
im9=uint8(zeros(size(im)));
im10=uint8(zeros(size(im)));
im11=uint8(zeros(size(im)));
im12=uint8(zeros(size(im)));
im13=uint8(zeros(size(im)));
im14=uint8(zeros(size(im)));
im15=uint8(zeros(size(im)));
im16=uint8(zeros(size(im)));for xp=1:b;
for yp=1:a;
im1(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=a:a*2;
im2(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=2*a:3*a;
im3(xp,yp)=im(xp,yp);
end
end
for xp=1:b;
for yp=3*a:4*a;
im4(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=1:a;
im5(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=a:2*a;
im6(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=2*a:3*a;
im7(xp,yp)=im(xp,yp);
end
end
for xp=b:2*b;
for yp=3*a:4*a;
im8(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=1:a;
im9(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=a:2*a;
im10(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=2*a:3*a;
im11(xp,yp)=im(xp,yp);
end
end
for xp=2*b:3*b;
for yp=3*a:4*a;
im12(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=1:a;
im13(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=a:2*a;
im14(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=2*a:3*a;
im15(xp,yp)=im(xp,yp);
end
end
for xp=3*b:4*b;
for yp=3*a:4*a;
im16(xp,yp)=im(xp,yp);
end
endfigure,imshow(im1)
% figure,imshow(im2)
% figure,imshow(im3)
% figure,imshow(im4)
% figure,imshow(im5)
% figure,imshow(im6)
% figure,imshow(im7)
% figure,imshow(im8)
% figure,imshow(im9)
% figure,imshow(im10)
% figure,imshow(im11)
% figure,imshow(im12)
% figure,imshow(im13)
% figure,imshow(im14)
% figure,imshow(im15)
% figure,imshow(im16)
% line(px1,py1)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im21=uint8(zeros(size(im)));
for m=1:b+50;
for n=1:a+30;
im21(m,n)=im1(round(BP’*),round(AP’*));
end
end
figure, imshow(im21)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im22=uint8(zeros(size(im)));
for m=1:b+10;
for n=a:2*a;
im22(m,n)=im2(round(BP’*),round(AP’*));
end
end
figure, imshow(im22)X=’;
Y=’;
XP=’;
YP=’;
MP=;%%%
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im25=uint8(zeros(size(im)));
for m=b+10:b*2;
for n=1:a+30;
im25(m,n)=im5(round(BP’*),round(AP’*));
end
end
figure, imshow(im25)X=’;
Y=’;
XP=’;
YP=’;
MP=;
AP=MP^(-1)*X;
BP=MP^(-1)*Y;
im26=uint8(zeros(size(im)));
for m=b:b*2;
for n=a:2*a;
im26(m,n)=im6(round(BP’*),round(AP’*));
end
end
figure, imshow(im26)im31=im21+im22+im3+im4+im25+im26+im7+im8+im9+im10+im11+im12+im13+im14+im15+im16;
figure, imshow(im31)
line(,)
line(,)
line(,)
line(,)
bilineal.m
Mostrando bilineal.m.