… o com l’atzar està del teu costat per treure més nota
Aquestes fent un examen tipus test, hi ha quatre preguntes que no saps contestar i respondre erròniament et va a restar punts. Si decideixes contestar les quatre preguntes a l’atzar el més probable és acabar amb més punts que si no respons a cap. Aquesta afirmació sembla correcta, tenint en compte que si hi ha quatre preguntes amb quatre opcions de resposta és lògic suposar que el més probable és fallar tres vegades i encertar 1, si suposem que encertar suma un punt i fallar resta, en el cas més probable ens quedarem igual. Val la pena arriscar? ¿Passa el mateix amb un nombre diferent de respostes a l’atzar? Resulta que les matemàtiques tenen alguna cosa a dir a l’respecte …
Els exàmens de tipus test presenten una sèrie de respostes de les quals cal triar, normalment, una resposta correcta. En alguns exàmens tipus test hi ha més d’una resposta correcta, de vegades els errors resten punts, pot haver respostes ponderades o un límit de preguntes que es poden fallar.
Puc aprovar si faig un examen tipus test sense estudiar?
La idea d’aquest article és respondre a preguntes l’estil: Puc aprovar si faig un examen tipus test sense estudiar? La probabilitat està del meu costat si contesto aleatòriament? ¿Passa el mateix en qualsevol tipus de test? ¿Quina és la diferència si les fallades resten o si no? Quina probabilitat tinc d’aprovar si contesto la meitat a l’atzar? I si estic segur de la meitat? ¿I de treure un notable? I un excel·lent? …
Comencem en l’examen tipus test més senzill, els encerts sumen, les fallades i les respostes no contestades no afecten la nota.
Calculant la nota …
Definim alguns noms de variables:
N = Nombre total de preguntes ajudes a = Nombre d’encerts Anuncio n = Nota final
Si suposem que la nota és un número de el 0 a el 10 i l’examen té 10 preguntes al càlcul de la nota és trivial. La nota obtinguda és igual a el nombre de preguntes encertades:

… amb un barem
Si l’examen té un nombre de preguntes diferent a el barem de la nota, per obtenir la nota final cal dividir el nombre d’encerts entre el nombre de preguntes i multiplicar per límit superior de l’barem.
per exemple: Si el barem és de l’0 a 10 i hi ha 40 preguntes en l’examen, per treure maig 1 cal encertar 20 preguntes. És a dir, nombre de preguntes encertades entre nombre total: 20/40 = 0.5 i multipliquem el resultat pel límit superior de l’barem: 0.5 × 10 = 5.
Generalitzant, per calcular una nota en un examen tipus test en el qual no resten els errors i tenim un barem:
bₛ = Límit superior de l’barem

Calculant probabilitats …
És bastant obvi que independentment de si saps o no les respostes, si les fallades no resten punts, la millor opció és contestar a tot. Diguem que en qüestió de punts, no en tens, literalment, res a perdre.
En qualsevol cas, formalitzem l’assumpte amb una mica de matemàtiques, quantes combinacions de respostes són possibles? i de què depèn aquest número?
… amb una pregunta
El cas trivial és amb una única pregunta. Si tenim 4 opcions de resposta: a, b, c, d. Hi ha 4 possibilitats:

La probabilitat que ocorri un esdeveniment és el nombre d’esdeveniments possibles entre les vegades que ocorre l’esdeveniment en qüestió. En aquest cas hi ha 4 esdeveniments possibles, només 1 implica encertar i 3 fallar:
La probabilitat d’encertar responent a l’atzar una pregunta és d’una entre quatre: 1/4 = 0.25. Normalment diem un 25% de probabilitat d’encertar.
La probabilitat de fallar seria 3 entre quatre: 3/4 = 0.75. O sigui un 75%.
Com veiem, en aquest cas una resposta a l’atzar té totes les de perdre. També és interessant observar que si sumem les dues probabilitats obtenim el 100% ja que, en aquest cas, només hi ha dos resultat possibles: encertar o fallar. Veurem que aquest no és el cas si hi ha més d’una pregunta.
En resum …

… amb dues preguntes (o més)
amb dues preguntes podem contestar per exemple: a en la primera ja en la segona, a en la primera ib en la segona, ba la primera ja en la segona … aquestes són totes les possibles combinacions:
Aquests són, en definitiva, tots els esdeveniments possibles contestant a dues preguntes. Són 16. Quatre vegades més possibilitats que amb una pregunta. Aquest abril ve de el fet que tenim 4 opcions de resposta, i el que passa és que cada vegada que afegim una pregunta estem multiplicant per 4 les possibles combinacions de respostes:
p₁ = Nombre d’opcions de la pregunta 1 de p₂ = Nombre d’opcions de la pregunta 2 de c₂ = Nombre de combinacions de dues respostes
La fórmula seria:
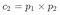
En aquest cas:

En general, simplement cal multiplicar pel nombre d’opcions, tantes vegades com preguntes hi hagi:

Aquesta fórmula és fàcil de simplificar, tenint en compte que el nombre d’opcions sempre és el mateix: p₁ = p₂ = p₃ = … = pₙ. Si definim:
n = Nombre de preguntes a p = Nombre d’opcions en cada pregunta
El nombre de combinacions es calcula així:

En aquest cas, amb p = 4 i n = 2:
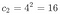
El següent pas és calcular les probabilitats . En aquest cas hi ha tres successos possibles:
- Encertar totes les preguntes.
- Encertar una pregunta (i fallar l’altra).
- Fallar totes les preguntes.
Tenint en compte tots els esdeveniments possibles, només hi ha un cas en el qual s’encerten totes les preguntes, suposant que les dues respostes correctes són la a:

Per tant la probabilitat d’encertar les dues preguntes és de 1/16 = 6.25%.
Generalitzant, la probabilitat d’encertar tot donat un nombre n de preguntes és d’1 entre totes les combinacions possibles de respostes, és a dir:


Una probabilitat d’un 6.25% ja és força baixa, però vegem com aquest percentatge disminueix dràsticament segons augmentem el nombre de preguntes que contestem a l’atzar. Per exemple, amb 10 preguntes:

Com veiem, hi ha més d’un milió de possibles combinacions, per tant, la probabilitat d’encertar totes les respostes a l’atzar és ínfima.
… de fet, és bastant més probable que et toqui la loteria .
Però no siguem tan ambiciosos, no cal encertar totes. Quina probabilitat hi ha d’encertar alguna? Suposant de nou que les respostes correctes són la a, aquestes són les vegades que encertem 1 responent a dues preguntes:

Cal notar que no hem ressaltat aa perquè són dos encerts, no un.
Comptem amb 6 possibles combinacions que ens donen una resposta encertada, la probabilitat està més del nostre costat:

la probabilitat d’encertar alguna cosa seria la suma de les dues anteriors, o el que és el mateix, afegir la possibilitat d’encertar tot a les possibilitats d’encertar 1:


No està malament, per haver contestat tot a l’atzar.
l’únic que ens queda és saber la probabilitat de fallar tot, i atès que és l’unic o succés que ens queda la probabilitat serà el que resti per arribar a el 100%, o el que és el mateix, la resta de combinacions possibles si restem els encerts:

Així que la probabilitat de fallar supera el cinquanta per cent, de manera que podem apostar que segurament no sumarem punts contestant dues preguntes a l’atzar.
I així quedaria la taula de resum afegint les probabilitats amb dues preguntes: