Intersecció
Siguin \ (S \) i \ (T \) subespais de el mateix espai vectorial \ (V \). Definim la intersecció de la manera següent:
\ (S \ cap T = \ left \ {{v \ in V \;: \; v \ in S \; \; \ wedge \; \; v \ in T} \ right \} \; \) intersecció de subespais
Propietat
\ (S \ cap T \) és subespai de \ (V \)
Demostració
1. \ ({0_V} \ in S \ wedge {0_V} \ in T \ Rightarrow {0_V} \ in S \ cap T \)
2. Considerem \ (u, \; v \; \ in \; S \ cap T \; \; \; \; \)
\ a \\] a \\]
de i es dedueix que \ (u + \; v \; \ in \; S \ cap T \; \; \; \; \)
3. Deixem a càrrec de l’lector demostrar:
\
Exemple 1
Siguin els subespais de \ ({\ mathbb {R} ^ 3} \):
\
\
Trobar \ (S \ cap T \).
Resolució
per definició \ (S \ cap T \) és un conjunt que estarà format pels vectors que pertanyin a \ (S \) ia \ (T \). És a dir aquells vectors que satisfacin les equacions de \ (S \) i les de \ (T \):
\
Es tracta d’ una recta definida com a intersecció de dos plans. Una base de la recta és un vector director.
Geomètricament podem buscar el vector director com el producte vectorial dels vectors normals als plans:
\
\
Llavors \ (\ left \ {{\; \ left ({3, – 2,1} \ right) \;} \ right \} \) és una base de \ (S \ cap T \).
una altra forma de resoldre-ho és buscar la solució de sistema d’equacions:
\
\
I llavors una altra vegada arribem a que \ (\ left \ {{\; \ left ({3, – 2,1} \ right) \;} \ right \} \) és una base de \ (S \ cap T \).
Exemple 2
Siguin els subespais de \ ({\ mathbb {R} ^ {2 \ times 2}} \):
\
\
Trobar \ (S \ cap T \).
Resolució
La intersecció de subespais està formada pels vectors que verifiquen les equacions d’aquests subespais.
què ha de complir una matriu per pertànyer a \ (S \)?
\
Què ha de complir una matriu per pertànyer a \ (T \)?
Ha de poder escriure com a combinació lineal d’: \ (\ left ({\ begin {array} {* {20} {c}} 1 & 0 \\ 2 & {- 1} \ end {array}} \ right) \; i \ left ({\ begin {array} {* {20} {c}} 1 & 0 \\ 1 & 0 \ end {array}} \ right) \)
Trobem les equacions de l’subespai \ (T \):
\
\
\
\
Ara plantegem que les matrius de \ (S \ cap T \; \) han de complir amb les equacions de \ (S \) i les de \ (T \):
\
O sigui:
\
Llavors les matrius de \ (S \ cap T \) són de la forma:
\
I una base de \ (S \ cap T \) és:
\
Hi ha un mètode alternatiu més breu per trobar una base de \ (S \ c ap T \) sense necessitat d’obtenir les equacions de \ (T \), com veurem a continuació.
Escrivim una matriu de \ (T \) com a combinació lineal dels vectors que la generen:
Però a més s’han de complir les equacions de \ (S \) que estableixen que \ (c = b \). Llavors:
\
Per tant, una matriu de \ (S \ cap T \) és:
\
Suma de subespais
Donats \ (S, \; T \; \) subespais de \ (V \), es defineix la suma així:
\ (S + T = \ left \ {{v \ in V \;: \; \; v = {v_1} + {v_2} \; \;, \; \; \, amb \; \; {v_1} \ in S \;, \; \; {v_2} \ in T} \ right \} \) suma de subespais
Propietat: \ (S + T \) és un subespai de l’espai vectorial \ (V \).
Deixem la demostració a càrrec de l’lector.
Si coneixem conjunts generadors de S i de T, podem trobar generadors de la suma:
\ (S = gen \ left \ {{{ v_1}, {v_2}, \ ldots, {v_q}} \ right \} \) i \ (T = gen \ left \ {{{w_1}, {w_2}, \ ldots, {w_r}} \ right \} \) \ (\; \ Rightarrow \; S + T = gen \ left \ {{{v_1}, {v_2}, \ ldots {v_q}, {w_1}, {w_2}, \ ldots, {w_r}} \ right \} \)
Per a trobar la suma és usual buscar les bases de \ (S \) i \ (T \). Com que les bases són conjunts generadors LI, si coneixem una base de cada subespai podrem obtenir un conjunt generador de la suma:
Donades les bases:
\ ({B_s} = \ left \ {{{v_1}, {v_2}, \ ldots, {v_q}} \ right \} \) i \ ({B_T} = \ left \ {{{w_1 }, {w_2}, \ ldots, {w_r}} \ right \} \)
Resulta:
\ (\ left \ { {{v_1}, \ ldots, {v_q}, {w_1}, \ ldots, {w_r}} \ right \} \) conjunt generador de la suma.
Observació: S’obté així un conjunt generador de la suma però no sempre és linealment independent.
- Quan LI, trobem una base de la suma.
- Quan LD, podem extreure una base de la suma eliminant els vectors “que sobren”.
Exemple 1
Donats els següents subespais de \ (V = {\ mathbb {R} ^ 3} \):
\
\
Ens interessa trobar \ (S + T \).
Busquem una base de \ (S \). Per això en l’equació aïllem una variable:
\
Ara armem un vector genèric:
\
\
Busquem una base de \ (T \). Per això en l’equació aïllem una variable:
\
Ara armem un vector genèric:
\
Llavors
\
\
Sabem que tot conjunt de més de 3 vectors en \ ({\ mathbb {R} ^ 3} \) és linealment dependent, ja que la dimensió de \ ({\ mathbb {R} ^ 3} \) és 3. Com podem extreure una base de la suma?
Podríem armar una matriu amb aquests 4 vectors i portar-la a la forma esglaonada. O si no, com l’espai és \ ({\ mathbb {R} ^ 3} \) podem pensar geomètricament:
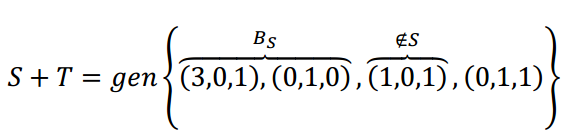
com \ (\ left ({1,0,1} \ right) \) no verifica l’equació de l’àmbit S, els 3 primers vectors no són coplanars i per tant formen una base de \ (\ mathbb {R} ^ 3 \). Podem eliminar \ (\ left ({0,1,1} \ right) \) perquè és combinació lineal d’aquesta base.
Per tant: \ (B = \ left \ {{\ left ( {3,0,1} \ right), \ left ({0,1,0} \ right), \ left ({1,0,1} \ right)} \ right \} \) és base de \ ( S + T \) i és base de \ (\ mathbb {R} ^ 3 \).
En aquest cas, com \ (S + T \; \) és un subespai de \ ({R ^ 3} \) de dimensió 3, podem afirmar que:
\
Generalitzant:
\ (S \) subespai de \ (V \) i \ (\ dim \ left (S \ right) = \ dim \ left (V \ right) \ Rightarrow S = V \)
Exemple 2
Donats els següents subespais de \ (V = {\ mathbb {R} ^ 4} \):
\
\
Trobar base i dimensió de \ ({S_1} + {S_2} \; \).
Resolució
\
\
\
\
\
Com hem vist, un mètode per analitzar si s on LI o LD, consisteix a armar una matriu amb els vectors com files i portar-la a la seva forma esglaonada. Per conveniència col·locarem els vectors en el següent ordre:
\ (\ left ({\ begin {array} {* {20} {c}} 1 & {- 1} & 0 & 1 \\ 1 & 0 & {- 1} & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ mathop \ to \ limits _ {{F_2} \ to {F_2} – {F_1}} \ left ({\ begin {array} {* {20} {c}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ mathop \ to \ limits _ {{F_3} \ to {F_3} – {F_2}} \ left ({\ begin {array} {* {20} {c}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \ end {array}} \ right) \)
\ (\ mathop \ to \ limits _ {{F_4} \ to {F_4} – {F_3}} \ left ({\ begin {array} {* {20} {c}} 1 & {- 1} & 0 & 1 \\ 0 & 1 & {- 1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \ end {array}} \ right) \)
La matriu esca lonada té 3 files LI (el seu rang és 3), llavors podem afirmar que la dimensió de \ (S + T \) es 3.
Com es va anul·lar l’última fila, el vector \ (\ left ({0,0,1,0} \ right) \) és combinació lineal dels altres tres, per tant una base de \ (S + T \) és: \ ({B_ {S + T}} = \ left \ {{\ left ({1, – 1,0,1} \ right), \ left ({0,1,0 , 0} \ right), \ left ({1,0, – 1,1} \ right)} \ right \} \).
Recordem que les files de la matriu esglaonada componen una altra base de la suma:
\
suma directa
la suma de dos subespais és directa si i només si la intersecció de els subespais és el vector nul.
\
Quan la suma és directa s’escriu:
\
Exemples en \ ({\ rm {V}} = {\ mathbb {R} ^ 3} \)
a continuació considerarem diferents casos de suma de subespais en \ ({\ mathbb {R} ^ 3} \).
Dues rectes
Un cas possible de suma de dues subespais en \ ({\ mathbb {R} ^ 3} \) és el de dues rectes que es tallen:
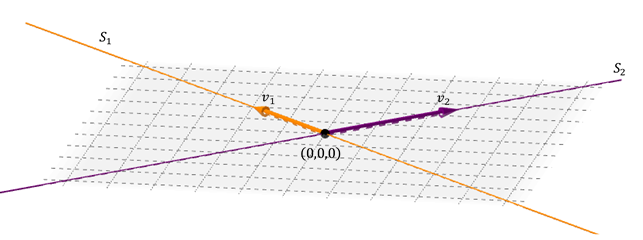
L us dos vectors LI de les rectes generen un pla: aquell que conté a les dues rectes. La suma és directa perquè la intersecció entre les rectes és el vector nul.
\
\ ( {S_1} \ oplus {S_2} = S \) on \ (S \) és el plànol que conté a les dues rectes
Dos plans que es tallen
Un altre cas possible de suma de dos subespais en \ ({\ mathbb {R} ^ 3} \) és el de dos plans que es tallen en una recta: a 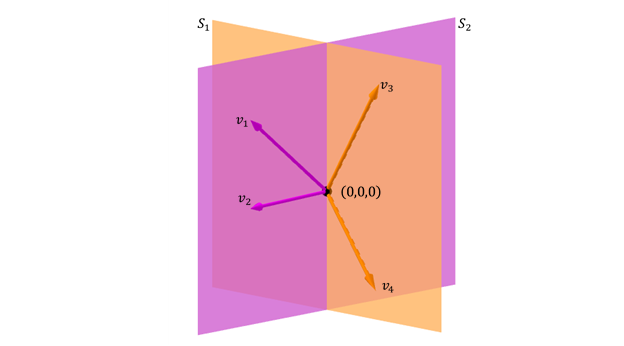
\}} = gen \ left \ {{\; {v_1}, {v_2}, {v_3}} \ right \} \]
la suma dels subespais és \ ({\ mathbb {R} ^ 3} \) però no és suma directa perquè la intersecció no és el vector nul:
\
Un pla i una recta inclosa en el pla
Un altre cas possible de suma de dues subespais en \ ({\ mathbb {R} ^ 3} \) és el d’un pla i una recta inclosa en el pla. 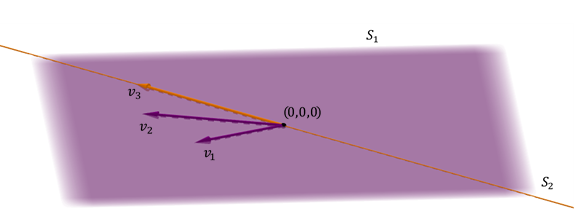
\
S’obté el mateix pla, i la suma no és directa perquè la intersecció no és igual a el vector nul.
Un pla i una recta no inclosa en el pla
Un altre cas possible de suma de dues subespais en \ ({\ mathbb {R } ^ 3} \) és el d’un pla i una recta no inclosa en el pla. 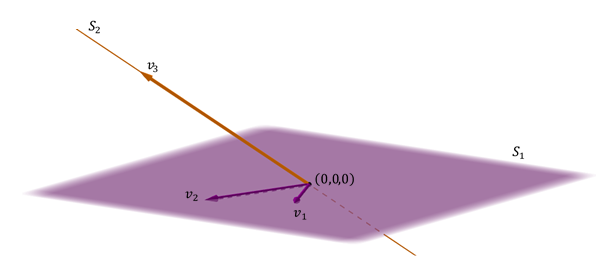
\
Es genera \ ({\ mathbb {R} ^ 3} \ ) perquè el vector director de la recta no és coplanar amb els vectors de el pla, ia més és directa perquè la intersecció és el vector nul:
\
Observació: En l’últim cas , la unió de les bases dels dos subespais forma una base de tot l’espai. En aquest cas, cada vector de \ ({\ mathbb {R} ^ 3} \) pot expressar-se de forma única com a suma d’un vector de \ ({S_1} \) i un altre de \ ({S_2} \).
Exercici per al lector març
Donats \ ({S_1} = gen \ left \ {{\ left ({1,2,1} \ right), \; \ left ( {0,2,0} \ right)} \ right \} \) i \ ({S_2} = \ left \ {{\ left ({x, y, z} \ right): \; \; \; x + i = i – kz = 0} \ right \} \),
a) Trobar els valors de \ (k \) pels quals \ ({S_1} \ oplus {S_1} = {\ mathbb {R} ^ 3} \).
b) Per \ (k = 0 \), comprovar que \ (v = \ left ({3,2,1} \ right) \) pot expressar-se de forma única com a suma d’un vector \ ({v_1} \ in {S_1} \) i un altre de \ ({v_2} \ in {S_2} \).
Exercici per al lector abril
Siguin els subespais de \ ({\ mathbb {R} ^ 4} \):
\ (S = gen \ left \ {{\ left ({1,1,1 , 1} \ right), \; \ left ({0,1,0,1} \ right)} \ right \} \) i \ (T = \ left \ {{\ left ({x, i, z , t} \ right): \; \; \; x – z = 0 \; \; \;, \; \; x – z + t = 0} \ right \} \)
Quina de les següents afirmacions és correcta? Justificar.
- \ (S \ oplus T = {\ mathbb {R} ^ 4} \)
- \ (S + T = {\ mathbb {R} ^ 4} \)
- \ (S + T = W \; \; \; i \; \ dim \ left (W \ right) = 3 \)
- \ (S \ oplus T = W \) i \ (\ dim \ left (W \ right) = 3 \)
Teorema de la dimensió de la suma
Si \ ({ S_1} \) i \ ({S_2} \) són subespais d’un espai vectorial \ (V \) (de dimensió finita), llavors:
\
En el cas particular que la suma sigui directa, com \ ({S_1} \ cap {S_2} = \ left \ {{{0_V}} \ right \} \) , resulta:
\
Exemple
Donats els subespais de \ ({P_2} \):
\
\
Trobar bases de tots dos subespais i de la intersecció
Resolució
Trobem una base de \ ({S_1} \):
\
Llavors són els polinomis de la forma:
\
Després una base de \ ({S_1} \) és:
\
Trobem una base de \ ({S _2} \):
\
Llavors són els polinomis de la forma:
\
\
Per a buscar \ ({S_1} \ cap {S_2} \) hem de plantejar que es compleixin les equacions de \ ({S_1} \) i també les de \ ({S_2} \):
\
Els polinomis seran de la forma:
\
Després:
\
Cal notar que com coneixem les dimensions de \ ({S_1} \), \ ({S_2} \) i \ ({S_1} \ cap {S_2} \), podem calcular la dimensió de \ ({S_1} + {S_2} \):
\
Però l’únic subespai de \ ({P_2} \) amb dimensió 3 és \ ({P_2} \) . Després: \ ({S_1} + {S_2} = {P_2} \).
Exercici per al lector 5
Donats els subespais de \ ({\ mathbb {R} ^ {2 \ times 2}} \):
\
\
a) Trobar bases de \ ({w_1} \) i \ ({W_2} \)
b) Obtenir \ ({w_1} \ cap {W_2} \).
c) Sense trobar \ ({w_1} + {W_2} \) analitzar la validesa de la següent afirmació:
\
d) Proposar una base de \ ({\ mathbb {R} ^ {2 \ times 2}} \) formada per matrius simètriques i antisimètrica, i expressar la matriu
\
com a suma d’una matriu simètrica més 1 antisimètrica.
Producte intern
a la primera unitat vam veure producte escalar entre vectors i les seves aplicacions a la Geometria. En aquesta secció ens proposem generalitzar aquesta operació a altres espais vectorials definint la noció general de producte intern a partir de les propietats del producte escalar.
Definició: Un producte intern en un espai vectorial real \ ( V \) és una operació que assigna a cada parell de vectors \ (u \) i \ (v \) de \ (V \) un nombre real \ (u \ ;. v \) tal que es verifiquen les següents propietats ( per a tot vector \ (u, \; v, \; w \) de \ (V \) i tot escalar \ (\ alpha \)): 1. \ (U \ cdot v = v \ cdot u \)
2. \ (U \ cdot \ left ({v + w} \ right) = \ left ({u \ cdot v} \ right) + \ left ({u \ cdot w} \ right) \)
3. \ (\ Alpha u \ cdot v = \ alpha \ left ({u \ cdot v} \ right) \)
4. \ (Uu \ ge 0 \; \; \; \ wedge \; \; \; uu = 0 \; \; \; \; \ Leftrightarrow \; \; \; \; u = {0_V} \)
És possible definir així diferents productes interns en qualsevol espai vectorial (mentre es verifiquen aquestes propietats). En la nostra matèria, només treballarem amb el producte intern canònic a \ ({\ mathbb {R} ^ n} \), que és l’extensió de l’producte escalar:
\ (\ left ({{x_1}, {x_2}, \ ldots, {x_n}} \ right). \ left ({{i_1}, {i_2}, \ ldots, {y_n}} \ right) = {x_1} {y_1} + {x_2} {i_2} + \ ldots {x_n} {y_n} \) producte intern canònic a \ (\ mathbb {R} ^ n \)
Aquesta definició ens permet estendre el concepte d’ortogonalitat a \ ({\ mathbb {R} ^ n} \):
\ (u \ bot v \; \; \; \ Leftrightarrow \; \; uv = 0 \) condició d’ortogonalitat
Exemple
Realitzem el producte intern dels vectors de \ ({ \ mathbb {R} ^ 4} \):
\
\
Com \ (uV = 0 \) llavors \ (u \) i \ (v \) són ortogonals. \ (\; \)
Complement ortogonal d’un subespai
sigui \ (S \) subespai de \ (V \) (espai vectorial amb producte intern).
El complement ortogonal de \ (S \), que denotem com \ ({S ^ \ bo t} \), és el conjunt de vectors de \ (V \) que són ortogonals a cada un dels vectors de \ (S \):
\ ({S ^ \ bot} = \ left \ {{\; v \ in V \;: \; \; v \ cdot w = 0 \; \; \; \; \ forall w \ in S \; } \ right \} \) complement ortogonal de \ (S \)
Propietat: \ ({S ^ \ bot} \) és un subespai de \ (V \).
1. \ ({0_V} \) pertany a \ ({S ^ \ bot} \) doncs \ ({0_V} .w \; = \; 0 \) per a tot \ (w \) de \ (S \)
2. Siguin \ (u, v \ in {S ^ \ bot} \ Rightarrow uw \; = \; 0 \ wedge vw \; = \; 0 \; \; \; \; \ forall w \ in S \ Rightarrow \ left ({u + v} \ right) .w \; = \; uw \; + \; v.w \; = \; 0 \)
Per tant \ (u + v \) està en \ ({S ^ \ bot} \)
3. Si \ (u \ in {S ^ \ bot} \ Rightarrow ku \ in {S ^ \ bot} \). Per què?
Exemple 1
Sigui \ (S = \ left \ {{\ left ({x, y, z} \ right) \ in {\ mathbb {R } ^ 3} \; | \; 2x + 3y – z = 0} \ right \} \). Trobar \ ({S ^ \ bot} \).
Resolució
Hem de buscar els vectors de \ ({\ mathbb {R} ^ 3} \) que siguin perpendiculars a tots els vectors d’aquest pla.
Primer vam buscar una base de \ (S \), per exemple:
\
Per a trobar el complement ortogonal, busquem tots els vectors \ (\ left ({x, y, z} \ right) \) que siguin ortogonals a \ (\ left ({- 1,, 1,1} \ right) \) ja \ (\ left ({0,1,3} \ right) \).
s’obté així un sistema d’equacions que defineix el complement ortogonal:
\
\
Quina és una base de l’subespai \ ({S ^ \ bot} \)?
\
La base és un vector perpendicular a l’àmbit \ (S \). Per tant, el complement ortogonal d’un pla que passa per l’origen és la recta perpendicular que passa per l’origen.
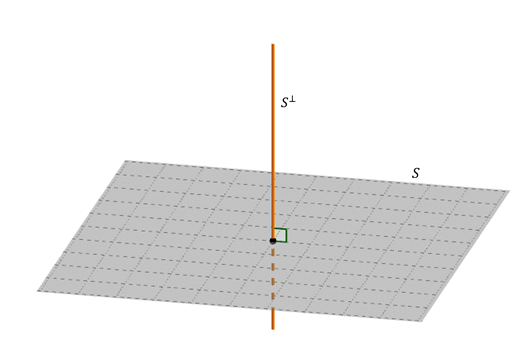
Si \ (S \) és una recta que passa per l’origen: quin és el seu complement ortogonal?
Exercici per al lector 6
per justificar el procediment que fem servir per trobar les equacions de \ ({S ^ \ bot} \), els demanem que demostrin la següent propietat:
Siguin \ (u, \; v, \; w \) vectors de \ ({\ mathbb {R} ^ n} \).
Si \ (w \) és ortogonal a \ (u \) ia \ (v \) , llavors és ortogonal a qualsevol combinació lineal d’\ (u \) i \ (v \).
Exemple 2
Atès següent subespai de \ ({\ mathbb {R} ^ 4} \):
\
Halle base i dimensió de l’complement ortogonal.
Resolució
Hem de buscar els vectors de \ ({\ mathbb {R} ^ 4} \) que són ortogonals als vectors de \ (S \).
Trobem una base de \ (S \ ):
\
\
Ara busquem els \ (\ left ({{x_1}, {x_2}, {x_3}, {x_4}} \ right) \) tals que:
\
trobem les equacions que defineixen a \ ({S ^ \ bot} \):
\
Busquem una base de \ ({S ^ \ bot} \):
\
\
Propietats de l’complement ortogonal
sigui \ (V \) un espai vectorial de dimensió finita, amb producte intern, i sigui \ (S \) un subespai de \ (V \). Llavors es verifiquen les següents propietats:
- \ ({\ left ({{S ^ \ bot}} \ right) ^ \ bot} = S \ )
- \ ({V ^ \ bot} = \ left \ {{\; {0_V} \;} \ right \} \) i \ (\ left \ {{\; {0_ {V \;}}} \ right \} {\; ^ \ bot} = V \)
- \ (S \ cap {S ^ \ bot} = \ left \ {{{0_V}} \ right \} \)
- \ (S + {S ^ \ bot} = V \)
Aquesta última propietat significa que qualsevol vector de \ (V \) pot expressar com a suma d’un vector de S més un altre de \ ({S ^ \ bot} \).
Il·lustrem amb un exemple geomètric de \ ({\ mathbb {R} ^ 3} \):
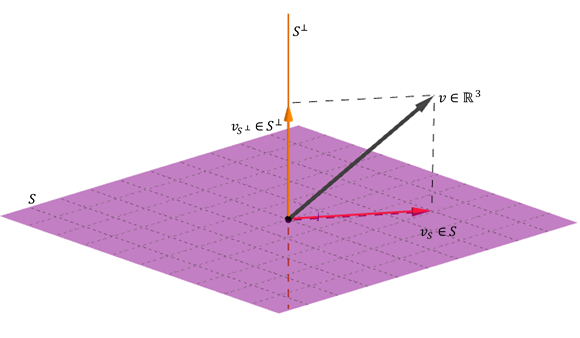
de les propietats 3 i 4 es dedueix:
I per tant:
La unió d’una base de \ (S \) amb una base de \ ( {S ^ \ bot} \) és base de \ (V \). Això s’aplica per estendre una base de \ (S \; \) a una base de \ (V \), com mostra el següent exemple.
Exemple
Sigui \ (S = \ left \ {{\ left ({{x_1}, {x_2}, {x_3}, {x_4}} \ right) \ in {\ mathbb {R} ^ 4} \;: \; \; {x_1} + {x_4} = 0 \; \;, \; \; {x_1} – {x_2} +3 {x_4} = 0 \;} \ right \} \).
Trobar una base de \ (S \) i estendre-la a una base de \ ({\ mathbb {R} ^ 4} \).
Resolució
Busquem una base de S, per exemple:
\
Com \ (dim \ left (S \ right) = 2 \), podem anticipar que: \ (dim ({S ^ \ bot} \)) = 4 – 2 = 2
A partir de la base de S, obtenim les equacions de \ ({S ^ \ bot} \):
\
I trobem una base de \ ({S ^ \ bot} \), per exemple:
\
Llavors unint les bases de \ (S \) i \ ({S ^ \ bot} \) resulta:
\ (B = \ left \ {{\ left ({1, – 2,0, – 1} \ right), \ left ({0,0,1,0} \ right), \ left ({2,1,0,0} \ right), \ left ({0,1,0, – 2} \ right)} \ right \} \) base de \ ({\ mathbb {R} ^ 4} \)
Exercici per al lector 7
Donats els següents subespais de \ ({\ mathbb {R} ^ 4} \):
\ (S = \ left \ {{\ left ({{x_1}, {x_2}, {x_3}, {x_4}} \ right) \;: \; \; {x_1} = 0 \; \;, \; \; {x_2} + 2 {x_3} = 0 \;} \ right \} \) i \ (W = gen \ left \ {{\; \ left ({1,0,0,0} \ right), \ left ({2,3, k, 0} \ right)} \ right \} \)
Trobeu els valors de \ (k \) pels quals \ (W = \; {S ^ \ bot} \).