Una de les fites que ha revolucionat els escacs en els últims 20 anys és l’aparició dels coneguts com “engines” o mòduls d’anàlisi. Avui dia, pràcticament tots els jugadors repassen la seva partida amb el “amic inhumà”, buscant els errors que s’hagin comès en la partida. Tal és així, que l’avaluació d’un mòdul és presa, en l’actualitat, com el més proper a “la veritat” que coneixem, de fet, no és estrany escoltar els aficionats, i professionals, fer comentaris de l’tipus: “Aquí tinc 0.20 d’avantatge “.
No obstant això, em trobo constantment que aquesta eina és mal, o molt malament, utilitzada per la majoria de jugadors; i això comporta que el treball realitzat davant de l’ordinador pot servir per a poc o més aviat res. Constantment veig que ni les anàlisis realitzades tenen valor (perquè contenen errors d’embalum, com ja us ensenyaré), ni les conclusions que es treuen d’ells serveixen per millorar el nostre joc i, el que és pitjor, que el mòdul perjudica la nostra manera de pensar en el tauler, perdent per exemple tota noció estratègica. Per això, escric aquesta sèrie d’articles sobre els motors d’anàlisi amb algunes idees i consells que ens poden ajudar a millorar.
FONAMENTS
Sóc d’aquestes persones que, per poder utilitzar una mica bé, necessito comprendre què és el que fa. Per això, en primer lloc, vaig a explicar, de manera esquemàtica i telegràfica, què és el que fa un motor per dins per oferir-nos aquestes variants i avaluacions.
En primer lloc, hem de comprendre que un mòdul d’anàlisi consisteix, bàsicament, en dos sub-programes (tècnicament parlaríem de subrutines, però el terme sub-programa crec que s’entén millor). La primera d’elles calcula totes les jugades legals a partir de la posició actual. La segona, pren cada posició i l’avalua mitjançant una funció d’avaluació. Aquesta converteix la posició que hi ha sobre el tauler en un nombre que serà l’avaluació. Finalment, el programa ordena totes les avaluacions de més a menys i ens dóna la jugada més ben situada en aquesta llista, que serà la jugada que proposa l’ordinador.
En l’argot, a cada posició se l’anomena node, i per això, si mireu la informació que ofereix el mòdul durant el seu càlcul, podreu veure en kN (Quilo nodes, és a dir, 1000 nodes) quantes posicions avalua el vostre ordinador per segon. Podeu fer-vos una idea de com de ràpid és el vostre ordinador (tècnicament vostre processador, que és el que calcula).
La funció d’avaluació és una de les “fórmules màgiques” de cada motor, i és el que caracteritza, essencialment, cada mòdul. Així que, quan trieu un motor, esteu bàsicament comprant aquesta funció d’avaluació. Normalment aquesta consisteix en un càlcul de l’material que hi ha al tauler, donar-li un nombre a la mobilitat o amenaces, i fins i tot molts d’ ells inclouen patrons per avaluar numèricament. per exemple Deep Blue afegia un “plus” numèric en cas que un peó de torre arribés a sisena prop de l’enroc rival (peó en h6 amb el rei negre enrocat en g8); o el mòdul Crafty té un patró per reconèixer a un alfil tancat en h2 quan el rival juga g3 (com en la famosa partida Spassky-Fischer). Per això, treballar amb diferents mòduls m’ofereix diferents jugades per a una mateixa posició, perquè cadascú avalua a la seva manera.
Els números que assigna la funció d’avaluació són totalment arbitraris, ja que l’únic que importa és què node té la major avaluació. No obstant això, els programadors han canviat l’escala d’aquests números perquè tinguin certa relació amb el que els humans entenem (peó = 1 punt). Però compte, cada funció d’avaluació és diferent, i no podem comparar “a pèl” els números d’un i altre mòdul. Aquest és un dels primers errors que he detectat entre els jugadors, i que hem d’evitar. Tampoc podem prendre la valoració com un nombre absolut, “tenir 0.25” no vol dir res, més que, per la mobilitat de les peces, és probable que la nostra posició sigui més còmoda; però aquesta no és la informació que necessita un jugador de torneig: si té avantatge, com s’executa, si és suficient per guanyar, quin tipus de posició l’espera, etc.
FONS, PLY I CÀLCUL BRUT
els programadors es fan la mateixa pregunta que ens fem els jugadors, ¿quan deixar de calcular i simplement avaluar la posició ?. A l’igual que ens passa a nosaltres, la resposta no és fàcil. Per això, l’ordinador va calculant en “nivells de profunditat”, a mesura que li deixem temps per calcular una posició, va arribant més lluny en el seu càlcul.
Els nivells de profunditat es mesuren en “ply”, que és el que en escacs considerem “mitja jugada” (que jugui el blanc o que jugui el negre); és a dir, si tinc una posició (node) i mitjançant una jugada d’el blanc arribo a una altra posició (node), totes dues posicions són a 1 ply de distància. Per tant, una profunditat de 2 ply implica que l’ordinador ha calculat totes les possibles posicions que es produeixen després d’una jugada d’el blanc i una de l’negre.
L’ordinador va progressant en aquesta profunditat. En primer lloc genera totes les possibles jugades legals, i per tant, genera tots els possibles nodes als quals podem arribar des de la posició actual. Després avalua tots aquests nodes i els ordena de millor a pitjor avaluació. Un cop fet tot això l’ordinador ha acabat de calcular a profunditat 1. Tot seguit, agafa totes les posicions generades a un ply i calcula totes les possibles jugades legals, generant tots els possibles nodes als quals arribarem després de 2 ply, i els avalua; així haurem arribat a profunditat 2; i així successivament.
A aquest procés que us he descrit se l’anomena càlcul brut.
CÀLCUL SELECTIU
El càlcul brut és formalment correcte, el que passa és que el nostre ordinador es veu obligat a calcular TOTS els possibles posicions que sorgeixen de cada jugada, de manera que moltes vegades estarà perdent el temps en posicions absolutament perdudes (amb dama i dues torres a faltar, per exemple).
Una idea per millorar el rendiment dels motors és utilitzar el que s’ha anomenat el càlcul selectiu. En ell, l’ordinador calcula totes les possibles jugades i les avalua; però només selecciona unes poques, les millors, per realitzar el següent nivell de profunditat. Posem per exemple que el “nivell de selectiu” és tres; llavors l’ordinador pren les tres posicions que han portat a les tres millors avaluacions i genera totes les possibles jugades des d’aquestes tres posicions (nodes). Ara, avalua les jugades i torna a triar les tres millors per calcular totes les posicions de el següent nivell de profunditat, i així successivament.
el càlcul selectiu és molt més ràpid que el càlcul brut. a més, es basa en la forma en que calculen els humans quan trien les jugades candidates. No obstant això, corre el risc de deixar-se variants interessants al tinter. Si una jugada lliura la dama per donar mat 5 jugades més endavant, difícilment podrà estar entre les tres millors de la posició en el nivell de profunditat 1 . És més, l’ordinador hauria d’arribar a un nivell de profunditat setembre (brut) per poder veure el mat.
Com s’ajusta el nombre de jugades que volem en el selectiu ?, la majoria d’ordinadors compten amb un paràmetre que és “nombre de línies de càlcul”. Doncs bé, cada vegada que aquí poseu 1, 3 o 10 esteu ajustant el nombre de jugades candidates que utilitza el vostre ordinador en el selectiu.
CÀLCUL BRUT / SELECTIU
Per aprofitar el millor dels dos mons, els programadors han optat per un càlcul mixt, que combina el brut i el selectiu. L’ordinador primer calcula en brut fins a un nivell de profunditat, i abans de passar a el següent, realitza un càlcul selectiu a major profunditat. És a dir, l’ordinador calcula en brut fins profunditat 20, i després agafa les tres primeres i segueix aprofundint fins a 33 amb la tècnica de el càlcul selectiu; després fa el càlcul brut a profunditat 21, i torna a fer el selectiu; i així successivament.
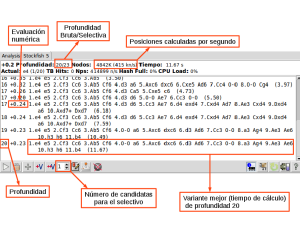
Per això, quan mireu en la informació de la lliçó a l’apartat profunditat aneu a veure una fracció 20/33, que significa nivell 20 de profunditat en càlcul brut, nivell 33 en selectiu.
Alguns motors d’anàlisi confien poc en el selectiu (per exemple Stockfish), mentre que altres creuen que és el més important (Houdini). De moment només us diré que és molt important que, en cada càlcul que feu, tingueu present aquests números, perquè ens diran quant ha aprofundit l’ordinador i com d’assegurances podem estar d’el resultat que ens ofereix.
vELOCITAT CPU i HASH TABLE
Finalment, comentarem dos aspectes “físics” del nostre ordinador: la velocitat de la CPU i la Hash Table. l’ordinador té un processador, que és el que calcula ( això és, el que realitza operacions sobre els “números” que entren i ofereix uns números en la seva sortida). Aquesta velocitat són, ara, els famosos GHZ que apareixen. Per exemple, un Pentium 4 a 3 GHz vol dir que l’ordinador té una “velocitat” de 3GHz. Si teniu un ordinador més ràpid, en la funció de càlcul de nodes i d’avaluació, el vostre ordinador ho farà més ràpid, i per tant, arribarà a més nivells de profunditat en menys temps.
Vull subratllar que, MANERA, un processador millor (més ràpid) implica que el vostre ordinador trobarà millors jugades.Qualsevol ordinador vell, si li donem temps suficient, trobarà la mateixa jugada per al mateix nivell de profunditat, que l’ordinador més ràpid de l’món (amb el mateix motor d’anàlisi).
Tots aquests càlculs i avaluacions que fa l’ordinador els emmagatzema en la memòria, perquè en el següent nivell de profunditat, en lloc de començar des de 0 els càlculs, l’ordinador utilitza el calculat en el nivell anterior per afegir “una jugada més” (és molt més ràpid, òbviament) . el problema és que l’ordinador té tres nivells de memòria (en termes bàsics): Cache, RAM i disc dur. la memòria memòria cau és la que està “més a prop” de l’processador, sol ser petita, i serveix perquè l’ordinador deixi aquí emmagatzemats resultats intermedis mentre fa els càlculs. És la d’accés més ràpid. La memòria RAM és un pas intermedi, és d’accés bastant ràpid, i és on la majoria de programes s’executa al nostre ordinador. El disc dur és, amb molta diferència, la més lenta, però és on guardem les coses de manera permanent.
Durant el càlcul de posicions d’escacs, l’ordinador genera una quantitat ingent d’informació (nodes, avaluacions ) que ha d’anar emmagatzemant en algun lloc. El cau s’omple molt ràpidament, de manera que la següent memòria a utilitzar és la memòria RAM, que té una capacitat finita i que, a mesura que avancem en profunditat, també s’omple. Finalment tenim el disc dur, que és molt lent per als nostres objectius.
La Hash Table és una taula que funciona com a índex de la memòria que fem servir, i que organitza tots els càlculs que ja hem fet, de manera que si l’ordinador vol trobar on està l’avaluació d’una posició, el primer que pregunta és a la Hash table si la té en l’índex; i si no, la calcula ell de nou.
La majoria de motors ens permet dimensionar (donar mida) a aquesta Hash table; és a dir, ens permet dir com de gran és el quadern de notes que pot utilitzar el nostre motor d’escacs per guardar les seves posicions i avaluacions. Si aquest quadern és molt gran, l’ordinador passarà molt de temps recorrent l’índex buscant si té la posició que vol calcular ara. Si és molt petit, l’ordinador constantment haurà de calcular posicions que pot haver calculat ja en el passat. Per tant, no és tan simple com donar-li el major valor possible a la Hash Table.
La regla general diu que si el nostre processador és molt ràpid, millor que la memòria no sigui molt gran (perquè li costa menys calcular de buscar en la memòria), mentre que si és lent hem de fer-ho a l’contrari. Alguns motors han publicat quin és el valor òptim de memòria amb què han de treballar. La meva experiència és que el millor és ajustar “a mà” aquests valors per optimitzar el rendiment.
Hi ha molts altres factors que hem d’ajustar quan treballarem escacs amb un ordinador: emprar els compiladors adequats, triar la forma de compilar el motor, etc. Un motor ben optimitzat pot suposar una millora de l’40% en termes de velocitat de processament (Kilonodos per segon).
en el següent article, una vegada que tenim els fonaments, i entenem bàsicament com funciona, parlarem de com millorar el nostre treball amb ordinador.