A l’article Què és un Sistema Expert? Vam veure que consta d’una Base de Coneixements (BC), una base de Fets (BH) i un Motor (o Màquina) de Inferències (MI). I que aquests sistemes no es mesuren per la quantitat d’instruccions o programes sinó per la quantitat de regles que hi ha continguda en la seva Base de Coneixements.
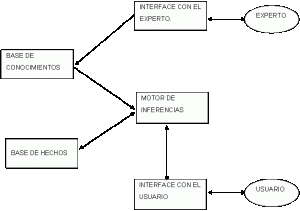
Vegem com es representen les regles
representació a través de regles:
Si H1 i / o H2 i / o H3 … llavors H4 i / o H5 …
Exemples: amor Si H1 i H2 llavors H3 i H4.
Si H3 o H4 llavors H5 i H6 o H7.
Si H2 i H7 o H6 llavors H9.
Vam veure que en prolog les regles de l’tipus: amor Si H1 i H2 i H3, … llavors Hc (Si es compleixen tots els fets llavors es compleix la conclusió).
es representen com : amor Hc si H1 i H2 i H3 … (Perquè es compleixi la conclusió s’han de complir els següents fets).
i la sintaxi és la següent: a Hc: – H1, H2 , H3, …
On els fets són predicats que s’han de complir.
R1: Si X > 3 i i = 5 llavors Z = 3 i A < 5.
En cas que X no sigui més gran que 3 la regla falla i es busqués una altra regla. En aquesta cas s’ha de complir dues condicions (per a la X i la Y) .. a Si la regla es compleix s’executa l’acció per Z i A.
R2: Si X2 llavors Z = 7
Aquí si la primera condició falla (X < 5) es passa la segona condició. N’hi ha prou que es compleixi una de les dues condicions.
Els fets són afirmacions que es refereixen als conceptes (classes i objectes) ia les relacions (atributs) entre ells.
Exemples de representació dels fets en diferents aplicacions de la IA.
MYCIN
l’organisme és un bacteroride
< subjecte > < relació > < concepte >
la coloració de l’organisme és gram +
< atribut > < subjecte > < valor >
DENDRAL
ressonància espectral amb numero atòmic igual a número
< subjecte > < atribut > < valor
M1 (shell)
Millor color = negre a < expressió > = < valor >
PROLOG
Agrada ( maria, tennis) a < relació > (< concepte >, < concepte >)
EXSYS (shell)
< qualificador (acabat en verb) > < valor >
el cost de l’ordinador és el factor de major importància
Exemples de regles:
Regla 1: Si té espina dorsal a I té cua horitzontal a I té un forat per respirar a I té sang calenta.
I els petits són alimentandos amb llet materna a I els fills neixen directament vius a Llavors és un cetaci.
Regla 2: Si és un cetaci a I mesura més de 25 p ies a Llavors és una balena
Regla 3: Si és un cetaci a I mesura aproximadament 6 peus a I té l’aleta límit vertical a I té un nas roma-petita
I viu a prop de les costes a Llavors és una marsopa
Regla 4: Si és un cetaci a I mesura aproximadament 6 peus a I té l’aleta límit vertical a I té un nas en forma de bec a I viu al mar a Llavors és un dofí
Regla 5: Si té espina dorsal a I té una aleta vertical a I respira a través de brànquies a Llavors és un peix.
Regla 6: Si és un peix a I té l’aleta límit triangular a I té la boca sota del cap a Llavors és un tauró
Observin que van definir les regles per als cetacis ia partir d’aquesta es va definir a el dofí, la balena, etc. Igual va succeir per als peixos.
Com busquen els sistemes experts?
Sabem donat un estat inicial, es van generant estats a través de l’aplicació d’un conjunt de regles, les quals a l’aplicar-se originen un nou estat, així successivament fins arribar a l’estat final.
Hi haurà en conseqüència un estat inicial i un estat final que seran definits com:
1. Una base de fets en la qual apareixerà un fet que satisfà certes característiques. De 2. Una base de fets en la qual hauran desaparegut tots els fets a establir. De 3. Una base de fets tal que cap regla pot aportar una nova modificació.
Els punts 1 i 3 són comunament adoptats pels motors de encadenament cap endavant, mentre el 2 és adoptat per motors amb encadenament cap enrere.
Exemple de cerca primer en profunditat
Prenguem l’exemple de les tines, on es parteix de dues tines (recipients per contenir aigua) i es vol aconseguir que la de 4 galons tingui 2 galons. Les tines no tens marques que indiquin la quantitat de galons.
Anem a definir algunes regles de forma general: a Restriccions de 1) “Si una tina es ple fins al límit, no omplir la una altra “. de 2)” Si una tina s’acaba d’omplir fins al límit, no es pot botar “. Ordre de les regles: a 1r. Aplicar regles per al criteri de solució.
2on. Aplicar regles per omplir les tines.
3r. Aplicar regles per buidar d’una per a una altra. A 4t. Aplicar regles per botar el contingut d’una d’ella.
Criteri de solució a R1: Si (la tina de 4) (té) (dos galons) llavors SOLUCIÓ.
R2: Si (la tina de 3 ) (té) (dos galons) i (la tina de 4) (està buida) llavors (buidar el contingut) (per) (la tina de 4) a R3: Si (la tina de 3) (té) ( dos galons) i (la tina de 4) (no) (està buida) llavors (botar el contingut de) (la tina de 4)
Vegem com es va efectuant la recerca pas a pas
Estat inicial: (0,0) les dues tines buides de l’Estat 1: (0,0) – > (0,4) s’omple una de les tines (la de 4 galons). de l’Estat 2: (0,4) – > (3,1,) Es buida el contingut de la de 4 en la de 3 galons . de l’Estat 3: (3,1) – > (0,1) Es bota el contingut de la tina de 3 galons de l’Estat 4: (0,1 ) – > (1,0) Es buida el contingut de la de 4 en la de 3 galons. de l’Estat 5: (1,0) – > (1,4) s’omple la tina de 4 galons. De l’Estat 6: (1,4) – > (3,2) Es buida la tina de 4 en la de 3 galons de l’Estat final (3 , 2) s’arriba a la solució a l’quedar 2 galons a la tina de 4
Podeu veure aquest exemple en executi un sistema sistema expert en HTML