Desviació típica: Per a què serveix i com es calcula?

Segurament, en algun moment durant el teu pas pel col·legi vas tenir algun professor que et va ensenyar el que era la desviació típica a la classe de matemàtiques i fins i tot pot ser que ho hagis vist en alguna assignatura d’estadística, ¿Descobrim què és i com es calcula?

és molt possible és que, com tantes coses que vas aprendre durant la teva etapa escolar i que has oblidat, a dia d’avui i amb el pas el temps, ja no ho recordis. I és que la veritat és que és una mica del més normal i més comú del que sembla!

També és possible que et soni el concepte però, que si algú et demanés calcular-ho, no sabessis per on començar, perquè el més segur és que no estiguis molt familiaritzat amb la desviació típica ja que efectivament no és una cosa que haguem de fer servir cada dia. Sigui quin sigui el teu cas però, no t’has de preocupar perquè a continuació trobaràs tota la informació que necessites saber per refrescar la teva memòria i poder tornar a calcular aquesta mètrica sempre que ho necessitis.

Què és exactament la desviació típica ?

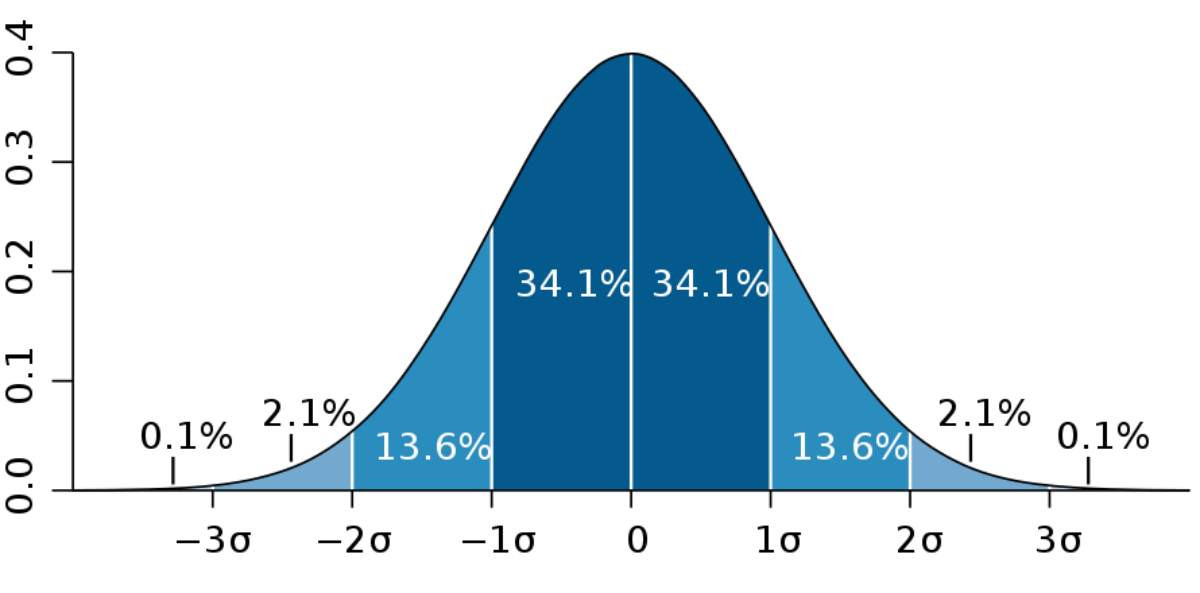
Doncs no és altra cosa que la mesura de dispersió que s’usa en estadística quan necessitem obtenir els resultats relatius tant per a variables quantitatives com per a variables d’interval que siguin el més aproximats possibles a la població o, en altres paraules, l’arrel quadrada de la variància de la variable.

Si vols entendre-la bé, és important que sàpigues que et serà de gran ajuda comprendre primer altres conceptes com la desviació estàndard i la variància, així familiaritza’t primer amb ells abans d’intentar calcular la desviació típica sense cap referent.

Quan ho hagis fet, fer els càlculs relatius a l’arrel quadrada et serà molt més senzill i podràs per fi conèixer la desviació que presenten les dades en la seva distribució respecte a la mitjana aritmètica d’aquesta distribució, que és l’objectiu últim d’aquesta mesura de dispersió.

En conclusió, la desviació típica del que ens permet és tenir una visió més d’acord amb la realitat en el moment de prendre les decisions i això és d’allò més interessant i útil no només per poder fer prediccions que afectin el futur d’un negoci (i en conseqüència a la quantitat de diners que es inverteix en una acció concreta i que amb aquesta podrem guanyar).

També per conèixer millor les tendències més repetides en un cert grup de la població com quin programa de televisió és el més vist o quin és el nombre de germans més comú que tenen les persones i fins i tot per a calcular la probabilitat que hi ha d’obtenir un resultat concret en una tirada de daus!

Alguns detalls que has de saber abans de començar a fer el càlcul

Per identificar-la en qua er context alguna cosa que has de tenir en compte és que qeneralmente sempre la trobaràs representada com σ, i que hi ha algunes propietats de les que hem de ser conscients, com el fet que si a tots els valors de la variable se’ls suma un nombre la desviació típica no varia i que aquesta sempre serà un valor positiu o zero en el cas que les puntuacions siguin iguals.

Tingues també en compte que si tots els valors de la variable es multipliquen per un nombre la desviació típica quedarà multiplicada per aquest nombre, i finalment, que si tens diverses distribucions amb la mateixa mitjana i coneixem les seves respectives desviacions, amb això ja podràs calcular la desviació típica total.

Quina és la forma correcta de calcular la desviació típica?

Encara que gràcies a Internet avui en dia tenim múltiples eines al nostre abast que ens permeten resoldre certes preguntes matemàtiques amb només introduir algunes dades en un sistema que calcula la dada específ ico que necessitem, mai està de més saber com calcular la desviació típica de forma manual perquè no tenir connexió a Internet no sigui un problema; és per això que, a continuació, t’expliquem com fer-ho.

El primer que hem de fer per poder calcular la desviació típica de la manera correcta és calcular la mitjana de les dades, així que si per exemple hi ha dos persones, un que mesura 1,50 i un altre que mesura 1,60, la mitjana serà 1,55, que és el punt mig entre els dos ‘encara que tingues en compte que pot ser que en algun cas no tinguis dades reals sinó intervals! Però també pots descobrir la desviació típica amb ells.

Un cop sabem la mitjana, hem de calcular la variància, sumant la marca de classe i restant-li a aquesta la mitjana de les dades a el quadrat pel nombre de dades que es corresponen per cada dada (f sub i) partit de l’nombre de dades que s’agafen (n).

Així que hem d’anar restant a la marca de classe, la mitjana que hem calculat abans i una vegada que la tinguem, farem el quadrat i multiplicarem cada un per cada freqüència de cada dada per sumar- ho tot a al final i finalment dividir-lo entre el nombre de dades que hi ha.

Recorda que en aquest punt , per obtenir la desviació típica ja només et caldrà calcular l’arrel de la variància ¡ i llest !

ja només has de ser conscient que una desviació baixa indicarà que la majoria de les dades s’acumulen al voltant de la mitjana aritmètica, però no obstant això , obtenir una desviació típica alta significarà que hi ha molta dispersió en els nostres dades i que els valors són molt extrems.

Rebre les últimes notícies Unsubscribe de les últimes notícies