Demostració de les fórmules de l'àrea i volum utilitzant integrals

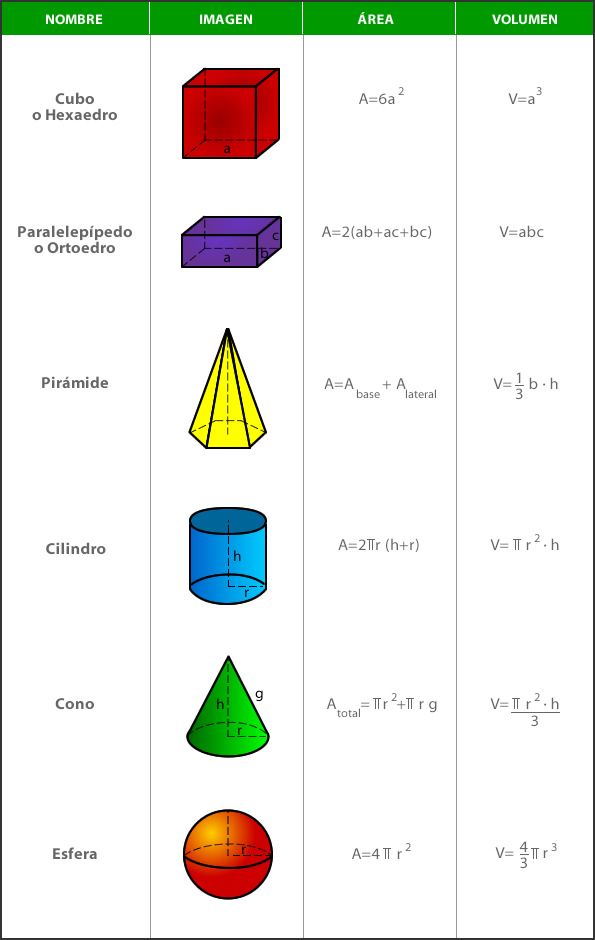
Bones! En aquesta entrada es demostrarà matemàticament les fórmules que tots coneixem d’àrea i volum de cossos coneguts com cubs, cercles, esferes, piràmides …

Per a això, és clar, emprarem la integració numèrica, una eina matemàtica essencial per qualsevol tipus de càlcul que inclogui una suma infinitesimal de diferents valors.

Per poder comprendre a la perfecció determinats càlculs exposats cal saber com a mínim integrar en una variable , i és molt recomanable visitar aquest article: Integrals dobles i triples. Canvis de variables

Taula de continguts

Les fórmules

Per calcular una àrea o volum, el que es fa és calcular la integral (Simple, doble, triple, curvilínia, de superfície …) de la funció constant f = 1 sobre el recinte les dimensions volem calcular.

Paral·lelepípede

Emprar integrals per a aquest cos geomètric és equivalent a matar mosques a canonades; no obstant això, com a primera utilitat bàsica de les integrals dobles i triples anem a calcular el seu volum

Volum

El nostre recinte d’integració és un paral·lelepípede de costats a, b i c. Per tant, la integral queda:

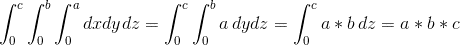
Cercle

tothom coneix les seves fórmules:

$2 \ pi r$ i $\ pi r ^ {2}$ . Però, com es dedueixen?

Primer de tot, cal saber que si volem representar gràficament una funció amb forma de circumferència no es pot representar tan fàcilment de la forma y = f (x) ja que no és injectiva, és a dir, per un valor de x apareixen 2 valors de i (La fórmula general per a un radi ri centrat en l’origen de coordenades és

$x ^ {2} + i ^ {2} = r ^ {2}$ . (En el cas de voler pintar un cercle, només cal canviar = per < =). per això s’empra la parametrització:

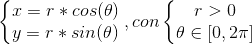
Demostració de les fórmules de l'àrea i volum mitjançant integrals 2

Que el seu determinant jacobià, per al canvi de variables és: r

Si vols saber més de la circumferència i com s’obté la seva fórmula d’una manera més detallada, aquest és el teu article

Aquí pots jugar una mica amb l’equació de la circumferència: Enllaç a Desmos

Perímetre

El r ecinto és aquest “filferro” que conforma la vora externa de l’cercle. Per tant, la corba parametritzada d’aquest filferro és:

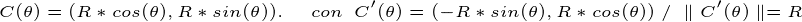
Demostració de les fórmules de l'àrea i volum mitjançant integrals 3

Calculant la integral curvilínia sobre la funció constant f = 1 — >

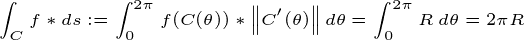
àrea

per calcular l’àrea n’hi ha prou amb calcular la integral sobre el recinte delimitat per la circumferència. Per facilitar els càlculs passem de coordenades cartesianes (x, y) a polars (r,

$\ theta$ ) emprant el jacobià r per el canvi de variable. $\ int \ int_ {S} dxdy = \ int_ {0} ^ {R} \ int_ {0} ^ {2 \ pi} r DRD \ theta = 2 * \ pi \ int_ {0 } ^ {R} r dr = 2 * \ pi * \ frac {R ^ {2}} {2} = \ pi * R ^ {2}$

Esfera

En el cas de les esfera seves fórmules són una mica més desconegudes.

$\ frac {4} {3} * \ pi * r ^ {3}$ per al volum i $4 * \ pi * r ^ {2}$ per a l’àrea de la seva superfície.

A l’igual que amb el cercle, emprarem altres coordenades, les coordenades esfèriques. L’equació de l’esfera en cartesianes és

$x ^ {2} + i ^ {2} + z ^ {2} \ leq R$ .

La parametrització és:

$\ left \ {\ begin {matrix} x = r * sin (\ theta) * cos (\ phi) \\ i = r * sin (\ theta) * sin (\ phi) \\ z = r * cos (\ theta) \ end {matrix} \ right$ , amb $\ left \ {\ begin {matrix} 0 \ leq r \ leq R \\ 0 \ leq \ phi \ leq 2 \ pi \\ 0 \ leq \ theta \ leq \ pi \ end {matrix} \ right$

Que el seu jacobià és

$r ^ {2} * sin (\ theta)$

Aquí pots jugar una mica amb l’equació de l’esfera: Entra a Geogebra 3D i enganxa això en l’editor: Superfície (r * sin (u) * cos (v), r * sin (u) * sin (v), r * cos (u), o, 0, pi, v, 0,2pi)

Àrea

per calcular l’àrea, només cal calcular el recinte recorregut per la parametrització amb r = R.Calculem la integral fent el canvi de variable amb el jacobià.

$\ int \ int_ {S} dxdy = \ int_ {0} ^ {\ pi} \ int_ {0} ^ { 2 \ pi} R ^ {2} * sin (\ theta) d \ theta d \ phi = 2 * \ pi * R ^ {2} * \ int_ {0} ^ {\ pi} sin (\ theta) d \ theta = 4 * \ pi * R ^ {2}$

volum

Per al volum calculem la integral de tot el recinte

emprant les variables $DRD \ theta d \ phi$ $\ int \ int \ int_ {V} dxdydz = \ int_ {0} ^ {\ pi} \ int_ {0} ^ {R} \ int_ {0} ^ {2 \ pi} r ^ {2} * sin (\ theta) d \ theta dr d \ phi = 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ^ {R} r ^ {2} * sin (\ theta) d \ theta dr \ rightarrow$ $\ rightarrow 2 * \ pi * \ int_ {0} ^ {\ pi} \ int_ {0} ^ {R} r ^ {2} * sin (\ theta) d \ theta dr = \ frac {2} {3} * \ pi * R ^ {3} \ int_ {0} ^ {\ pi} sin (\ theta) d \ theta = \ frac {4} {3} * \ pi * R ^ {3}$

Piràmide

la forma de calcular el volum d’una piràmide és idèntica a la d’un paral·lelepípede; la complicació és establir els límits d’integració (el recinte).

Tirant de lògica, la coordenada z serà lliure, variant des de 0 a h. Les coordenades x i y dependran de la coordenada z quant als màxims valors que prenen, partint des -b / 2 ab / 2 com a màxim a la base i prenent com a valor únic 0 quan la z = h (pic de la piràmide) . Basant-nos en aquest plantejament, prenem els límits de les variables:

$\ left \ {\ begin {matrix} - \ frac {b} {2} * (1- \ frac {z } {h}) \ leq x \ leq \ frac {b} {2} * (1- \ frac {z} {h}) \\ - \ frac {b} {2} * (1- \ frac {z } {h}) \ leq i \ leq \ frac {b} {2} * (1- \ frac {z} {h}) \\ 0 \ leq z \ leq h \ end {matrix} \ right$

Volum

Calculem la integral sobre el recinte delimitat per dxdydz

$V = \ iiint_ {V} dxdydz = \ int_ {0} ^ {h } \ int_ {- \ frac {b} {2} * (1- \ frac {z} {h})} ^ {\ frac {b} {2} * (1- \ frac {z} {h}) } \ int_ {- \ frac {b} {2} * (1- \ frac {z} {h})} ^ {\ frac {b} {2} * (1- \ frac {z} {h}) } dz dy dx = \ int_ {0} ^ {h} b ^ {2} * (1- \ frac {z} {h}) ^ {2} dz = \ rightarrow$ $\ rightarrow = b ^ {2} \ int_ {0} ^ {h} (1+ \ frac {z ^ {2}} {h ^ {2}} - \ frac {2z} {h}) dz = b ^ {2} * _ {0} ^ {h} = b ^ {2} * = b ^ {2} * \ frac {h} {3}$

Con

El con és molt similar a la piràmide. Tanmateix, hem d’emprar coordenades polars per poder parametritzar correctament la base circular. Emprarem les variables

$\ z, \ r \ i \ \ theta$ . Seguint una deducció similar a la piràmide ens queda: $\ left \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq R * (1- \ frac { z} {h}) \\ 0 \ leq \ theta \ leq 2 \ pi \ end {matrix} \ right$

Volum

Calculem la integral sobre el recinte delimitat per dxdydz i fem el canvi de variable a polars amb jacobià r

$V = \ iiint_ {V} dxdydz = \ int_ {0} ^ {h} \ int_ {0} ^ {R * ( 1- \ frac {z} {h})} \ int_ {0} ^ {2 \ pi} r \ dzdrd \ theta = \ pi \ int_ {0} ^ {h} R ^ {2} * (1- \ frac {z} {h}) ^ {2} = \ rightarrow$ $= \ rightarrow \ pi * R ^ {2} \ int_ {0} ^ {h} (1+ \ frac {z ^ {2}} {h ^ {2}} - \ frac {2z} {h}) = \ pi * R ^ {2} * _ {0} ^ {h} = \ pi * R ^ {2} * = \ pi * R ^ {2} * \ frac {h} {3}$

que, com anticipàvem, a l’igual que la piràmide seva fórmula és

$àrea \ de \ la \ base * \ frac {Alçada} {3}$

cilindre

el cilindre és potser la figura més intuïtiva a l’hora de calcular l’àrea de la superfície i el seu volum. Tot i ser obvi, anem a mostrar com es podria calcular el seu volum de forma integral (Sent, clarament, àrea de la base * altura) perquè es comprengui millor el funcionament d’integrals triples.

Farem servir les variables

$\ z, \ r \ i \ \ theta$ tal que: $\ left \ {\ begin {matrix} 0 \ leq z \ leq h \\ 0 \ leq r \ leq R \\ 0 \ leq \ theta \ leq 2 \ pi \ end {matrix} \ right$

Volum

Calculem la integral sobre el recinte delimitat per dxdydz i fem el canvi de variable a polars amb jacobià r

$V = \ iiint_ {V} dxdydz = \ int_ {0} ^ {h} \ int_ { 0} ^ {R} \ int_ {0} ^ {2 \ pi} r \ dzdrd \ theta = 2 \ pi \ int_ {0} ^ {h} \ int_ {0} ^ {R} r \ dzdr = \ rightarrow$ $\ rightarrow = \ pi * R ^ {2} * \ int_ {0} ^ {h} dz = \ pi * R ^ {2} * h$

Demostració de les fórmules de l’àrea i volum mitjançant integrals

Les fórmules

Paral·lelepípede

Volum

Cercle

Perímetre

àrea

Esfera

Àrea

volum

Piràmide

Volum

Con

Volum

cilindre

Volum

Deixa un comentari Cancel·la les respostes